In general, a non-central distribution is a transformation of a normal distribution. These transformation are defined by non-centrality parameters; If a non-centrality parameter (σ) is zero they are called central distributions. If σ is anything but zero, then they are non-central distributions.
The term “non-central distribution” may refer to one of several families of probability distributions:
Central vs. Non-Central Distributions
In elementary statistics, usually you’ll be dealing with the central versions of these distributions, which are special cases (with σ = 0) of the generalized distributions. These occur when the null hypothesis is true; They result in the tables found in the back of statistics textbooks.
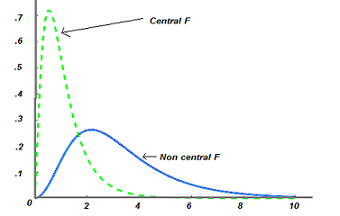
As an example, the F distribution results from a ratio of χ2 random variables divided by degrees of freedom. The central F distribution is a special case of the non-central F distribution where the numerator is a central chi-square random variable.
Use of Non-Central Distribution in Power Calculations
The non-central distribution is primarily used to calculate statistical power, although it can also be used to calculate confidence intervals on the standardized effect size Cohen’s d [2].
A non-central distribution occurs when the distribution shifts because the alternate hypothesis is true. More formally, the non-central distribution is defined by an NCP which measures “…the degree to which a null hypothesis is false” (Kirk, 2012). As the NCP increases, the distribution shifts to the right; The result is a larger percentage of the curve can be found to the right of the critical value for a chosen alpha level. In other words, increasing NCPs result in higher statistical power.
References
[1] Kirk, R. (2012). Experimental Design: Procedures for Behavioral Sciences. SAGE Publications.
[2] Cumming, G, How the noncentral distribution got its hump. Retrieved May 28, 2021 from: https://www.stat.auckland.ac.nz/~iase/publications/17/C106.pdf