Probability Distribution: List of Statistical Distributions >
What is the Johnson SU distribution?
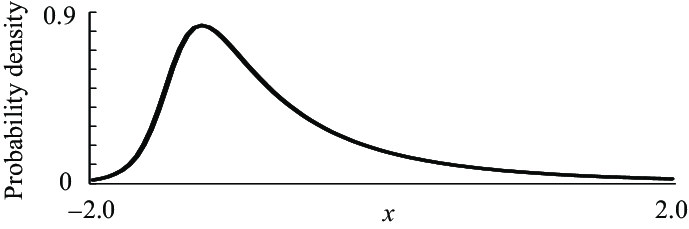
The Johnson SU distribution is an unbounded and continuous probability distribution. It is member of the Johnson system, a family of four probability distributions that also includes the lognormal distribution, the normal distribution, and the Johnson SB distribution. The “U” in the SU distribution stands for unbounded and the “B” in SB stands for bounded. Bounded distributions have constraints placed on them, like height, time, or weight maximums and minimums. Unbounded distributions do not have these restrictions.
The Johnson SU distribution can fit data that is leptokurtic and skewed [1]. That has made it useful in a variety of areas including modeling asset returns for portfolio management [2] and Value at Risk (VaR) modeling [3].
Johnson SU distribution PDF
Johnson [4] denoted the SU distribution as:
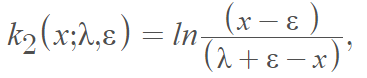
where the two shape parameters &lamdba; and ε are chosen to model a variety of distribution shapes.
References
Probability density image retrieved from https://www.researchgate.net/figure/Probability-density-function-of-the-Johnson-SU-distribution-d-1-g1-14-d1-10_fig2_356009022 under CC 4.0.
[1] Hossain, M. et al. (2019). Forecasting the General Index of Dhaka Stock Exchange. International Research Journal of Finance and Economics. January-February.
[2] Tsai, Cindy Sin-Yi (2011). “The Real World is Not Normal” (PDF). Morningstar Alternative Investments Observer.
[3] Choi, P. (2001). Estimation of value at risk using Johnson’s SU-normal distribution. Retrieved Januay 8, 2022 from: http://zoonek.free.fr/blosxom/Finance/2007-10-28_Articles.pdf
[4] Johnson, N. L. 1949. Systems of frequency curves generated by methods of translation. Biometrika 36: 149–176.