Statistics Definitions > Rician Distribution
What is a Rice/Rician Distribution?
A Rice or Rician distribution (also known as a Nakagami-n distribution) is one way to model the paths scattered signals take to a receiver. Specifically, this distribution models line-of-sight scatter — transmissions between two stations in view of each other that have an unobstructed path between them. Line-of-sight scatter includes FM radio waves, microwaves, MRI images in the presence of noise, and satellite transmissions. The distribution also models Rician fading, which is a way to show how signal cancellations affect radio propagation.
Properties of the Rice Distribution
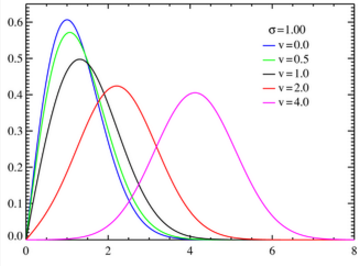
Two shape parameters define the Rician distribution: ν and σ. These, along with a third number, m, define the qualities of the probability density function. “m” controls the horizontal location of the distribution’s maximum value. The distribution is unimodal with thin tails (the tails decrease exponentially for large x-values).
The probability density function formula is:
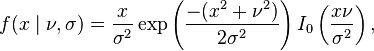
I0(z) is a modified Bessel function of the first kind with order zero.
The distribution is valid for real positive numbers. In other words, the interval for this distribution is {a, ∞) where a is any real positive number (real numbers are numbers that can be found on the number line).
Similar Distributions
This distribution is closely related to a number of other distributions, including the Beckmann distribution, Chi-Square distribution, Chi Distribution, Normal and Log Normal Distributions, Rayleigh distribution and Nakagami Distribution.
- The Rice Distribution is related to the normal distribution, because it is basically the distribution of the norm of two normally distributed variables.
- The pdf of the Rice distribution [ν, σ] is the same as the Beckmann Distribution with parameters [ν/√2, ν/√2, σ, σ].
- The pdf of the Rice distribution [0, σ] is the same as the pdf of the Rayleigh distribution [σ]
Rician distributions can only model non-dense, line-of-sight signals. Distributions that model dense scattered signals:
- Nakagami distribution.
- Rayleigh distribution.
Reference:
Gudbjartsson, H and Patz S. The Rician Distribution of Noisy MRI Data. Magn Reson Med. 1995 Dec; 34(6): 910–914. Available from Here.
Valkenburg, M. (1993). Reference Data for Engineers, Eighth Edition: Radio, Electronics, Computer & Communications 8th Edition. Newnes.