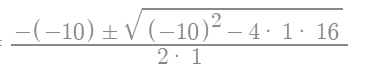In calculus, a curve is a mathematical object similar to a line, but it doesn’t have to be straight. A curve describes the path of a continuously moving point. As a practical example, an ellipse is a curve describing the motion of planets around a star.

Calculus originates from the study of curves and their properties; without curves, there would be no calculus.
Contents:
Calculus Curves: Classes
Many curves studied in calculus belong to certain classes of curves, sharing certain features and properties. In a way, you can think of these curves as the “famous” math curves; they have been studied extensively in ancient or modern times.
Algebraic curves are any curves that can be defined by a polynomial equation [1]. Quartic curves are given by a fourth degree polynomial (e.g. f(x) = x4).
Plane curves lies in a two-dimensional plane. In other words, the points of the curve are all on the same plane; you could draw these curves on a sheet of paper, unlike a 3D shape like a cube (you could draw this on a sheet of paper, but to be accurate you would really need to create a 3D model). In comparison, a space curve’s points do not necessarily all lie on a single plane [2].
Special curves have well-known features. They include circles, ellipses, and hyperbolas. However, there are many more obscure curves that are special. These include the Peano Curve and Quadratix of Hippias.
How To Articles
- Arc Length Formula
- Area Between Curve and Y-Axis
- Concave Up (Convex), Down
- Find the Area Under the Curve (Excel, Definite Integrals
- Intersections
- Linearization and Linear Approximation
- Normal Line
- Parameterize a Curve
- Quadrifolium
- Riemann Sums
- Secant Line
- Slope of a Curve
- Tangent Lines
- Tangent Vector (Velocity Vector)
Calculus Curves: A to Z
- Algebraic Curves
- Alysoid
- Ampersand Curve
- Astroid Curve
- Bean Curve
- Gaussian / Bell Curve
- Bow Curve
- Bullet Nose Curve
- Butterfly curve
- Cassini Oval
- Cissoid of Diocles
- Conchoid of Nicomedes
- Cruciform Curve
- Damped Sine Wave
- Deltoid Curve
- Devil’s Curve
- Eight Curve (Leminiscate of Gerono)
- Equiangular Spiral, Spira Mirabilis (Logarithmic Spiral)
- Fish Curve
- Folium of Descartes (Noeud de Ruban)
- Hippopede
- Hypocycloid Curve
- Kampyle of Eudoxus
- Klein Quartic
- Lamé curve
- Level Curve
- Lissajous Curves
- Lituus Curve
- Natural Equation of a Curve
- Nodal Cubic
- Pedal Curve
- Piriform Curve
- Plateau Curve
- Pursuit Curve
- Rectifiable Curve
- Rhodonea Curve (Rose Curve)
- Sawtooth Function (Wave)
- Serpentine Curve
- Simple Closed Curve
- Smooth Curve
- Spiric Section
- Tagaki Curve
- Tractrix Curve
- Trident of Newton
- Trifolium Curve
- Witch of Agnesi
Calculus Curves: References
Kepler orbit WillowW,
[1] Degree of a Curve. Retrieved February 27, 2022 from: http://assets.press.princeton.edu/chapters/s9665.pdf
[2] Montoya, D. & Naves, D. On Plane and Space Curves. Retrieved January 15, 2022 from: https://web.ma.utexas.edu/users/drp/files/Spring2020Projects/DRP_Final_Project%20-%20Daniel%20Naves.pdf
Curve sketching
Back in the day, curve sketching by hand was an important part of precalculus. But with the advent of the graphing calculator, sketching curves by hand isn’t usually necessary any more. Graphing calculators are allowed on most calculus exams (even AP Calculus), so you can graph your function on the TI-89 to get an idea of the overall shape. Then it’s just a matter of labeling the curve.
You may be asked to specifically include:
- X-intercepts,
- Y-intercepts,
- Horizontal asymptotes,
- Vertical asymptotes,
- Critical Points (maximums and minimums),
- Points of inflection,
- Endpoints.
See also: Using stationary points for graph sketching.
Read on for detailed information about how to find each of these important graph parts.
1. Curve Sketching: Finding X-intercepts
X-intercepts are where the function crosses the x-axis. These points are called roots or zeros. There are many ways to find roots, including on the TI-89 and using the rational number theorem. See the main roots/zeros article for more details on how to solve for a function’s roots.
You can also find roots for curve sketching with the quadratic formula. This requires you to have some strong algebra skills (including the ability to recognize when you can use the quadratic formula, and when you cannot).
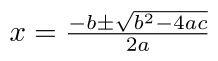
Example question: Find the zeros of this function algebraically: f(x) = x2 – 10x + 16
- Set f(x) to zero: 0 = x2 – 10x + 16,
- Identify a, b, and c. A quadratic function, like this one, has the form ax2 + bx + c = 0. So, a = 1, b = -10, c = 16.
- Plug a, b, and c values into the quadratic formula:

- Solve, using algebra, to get two roots: 8 and 2.
If you’re algebra is a little rusty, check out Symbolab’s calculator, which shows the steps for this solution.
2. Finding Y-intercepts
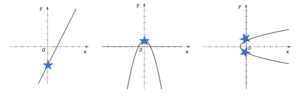
The next important topic in curve sketching: you’ll want to find where your graph crosses the Y-axis. To find the y-intercept, set x to zero and solve.
For example: y = x2 + 5x
Set x to zero and solve: y = 02 + 5(0) = 0
This function’s y-intercept is at x = 0.
For a quadratic equation, the y-intercept is the point “c”:
y = ax2 + bx + c
For example, y = 10x2 + 5x + 9, the y-intercept is 9.
In calculus, you won’t see more than one y intercept, because it creates a major issue called “one to many.”
3. Horizontal asymptotes
See: Horizontal asymptotes
How to Find Asymptotes
4. Vertical asymptotes
5. Critical Points (maximums and minimums)
See:
How to Find Critical Points.
Finding minima and maxima with the second derivative test.
6. Points of inflection
See: Points of inflection
7. Endpoints
See: Endpoints
Curve Sketching: References
Khan, D. Cracking the AP Calculus AB & BC Exams. Random House Information Group. 2009.
Algebraic Curves
An algebraic curve is any curve that can be defined by a polynomial equation [1].
More precisely, an algebraic curve has the polynomial equation:
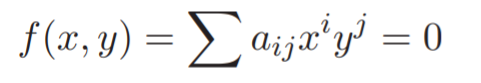
in x and y.
The degree of the algebraic curve is the degree of the polynomial f(x, y) [2].
The study of algebraic curves is one of the oldest fields of mathematics. The curves were widely used by the ancient Greeks, who used them to solve famous problems like the doubling of the cube (which requires solving the equation x3 = 2) or trisection of angles (which involves finding the intersection of a circle and a hyperbola) [3].
Examples of Algebraic Curves
The familiar quadratic curves (e.g. circles, ellipses, and parabolas) are algebraic curves, as are a variety of cubic curves, quartic curves, and many other curves of higher degree.
The simplest example of an algebraic curve is the solution set of a two-variable polynomial equation in two dimensions; for example, a parabola defined by y = a(x – h)2. A shape like a spiral is not algebraic, as it cannot be defined by a polynomial. Trigonometric functions like the sine function are also not algebraic, as they also cannot be defined by a polynomial (thanks to that tricky “π”, which isn’t the root of any polynomial with integer coefficients).
When a curve is not algebraic, the curve (and the function that defines it) is transcendental. Some of these curves are defined by special functions.
Defining the Algebraic Curve
The overview above describes the basic qualities of algebraic curves, but there are some unique characteristics that require a more precise definition. As the field has evolved over time, so has the multiplicity of language and symbols.
Algebraic curves are usually defined by complex numbers to ensure that the equations are unique. In math speak, that equates to a surface, or “objects of complex dimension 1.” Complex algebraic curves are orientable, which means they can be rotated in 3D space to produce spheres, donuts, and other surfaces. And they are usually (but not always) defined on the complex (affine) line [4]. However, a large part of the theory of algebraic curves applies to rational numbers as well [5].
References
[1] Degree of a Curve.
[2] Yan-Bin, J. (2017). Algebraic Curves. Retrieved Jan 22, 2022 from: https://faculty.sites.iastate.edu/jia/files/inline-files/algebraic-curves.pdf
[3] Algebraic Curves: A 2003 Math Circle Session by Renzo. Retrieved January 13, 2022 from: https://www.math.utah.edu/mathcircle/notes/curves.pdf
[4] Kerr, M. Algebraic Geometry III/IV.
[5] Gathmann, A. (2018). Plane Algebraic Curves: Class Notes TU Kaiserslautern. Retrieved Jan 22, 2022 from: https://www.mathematik.uni-kl.de/~gathmann/class/curves-2018/curves-2018.pdf
Hypocycloid Curve
A hypocycloid curve is a plane curve created by a point P on a small circle rolling around inside the circumference of a larger circle.
The parametric equations are [1]
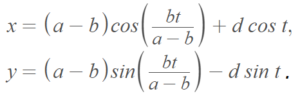
Cusps in the Hypocycloid Curve
Given that the larger circle’s diameter is a and the smaller circle’s diameter is b, we can define many unique hypocycloid curves. The ratio of a/b determines the number of cusps. For example, if the ratio is 3/1, the curve will have three cusps (i.e., it creates a deltoid curve).
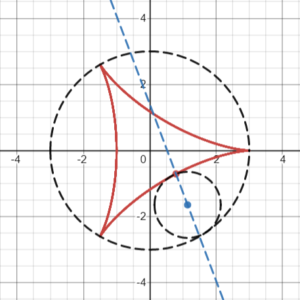
If the ratio a/b is irrational, many more elaborate and interesting curves can be created, some of which resemble multi-petaled flowers or star shapes [2].
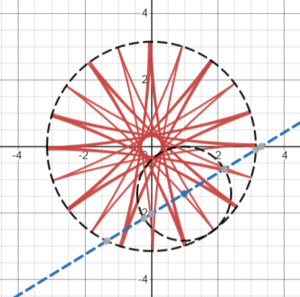
Check out this Desmos page, where you can change the values for a and b to create a variety of different shapes.
Many authors restrict a and b to integers. For example, for a rotating ring gear type epicycloid reducer (Shin) or designing hypocycloid gear assembly for internal combustion engines [3]. In engineering, the profile of some gear teeth is a combination of hypocycloid and epicycloid [2].
History of the Hypocycloid Curve
Albrecht Durer (1471 to 1528) was the first to introduce the hypocycloid curve in his four-volume, 1,525 geometry tome The Art of Measurement with Compass and Straightedge [4]. The curves were popularized in the latter half of the 20th Century with the invention of the Spirograph [5].

References
Petaled hypocycloid curve created with Desmos.
Spirograph image: Kungfuman,
[1] Chen, K. et al. (1999). Mathematical Explorations with MATLAB. Cambridge University Press.
[2] Parhusip, H. Arts revealed in calculus and its extension. International Journal of Statistics and Mathematics. Vol. 1(3), pp. 016-023, August, 2014.
[3] Bhattacharyya, B. (2013). Engineering Graphics. I.K. International Publishing House
[4] Simoson AJ (2008) Albrecht Dürer’s trochoidal woodcuts. Probl Resour Issues Math Undergraduate Stud (PRIMUS) 18(6):489–499
[5] Tsiotras, P. & Castro, L. Chapter 6 The Artistic Geometry of Consensus Protocols.
Simple Closed Curve
A simple closed curve is closed but does not intersect itself at any point. You could call it a non-self-intersecting continuous loop. A Familiar example is a circle.
It’s called closed because its first and last points are the same. It’s “simple” because it has no repeated points other than, perhaps, the first (which is equal to the last).
Simple closed curves are also known as Jordan curves. They are named after mathematician Camille Jordan (1838-1922), who first proved a groundbreaking theorem known as the Jordan curve theorem. This theorem tells us that every simple closed curve divides the plane to an interior region and an exterior region, and every continuous path connecting a point of one of these to a point of the other will intersect the curve somewhere. Although this might seem simple and obvious, it is actually very difficult to prove.
Examples of Simple Closed Curve
A circle is perhaps the simplest example of a Jordan curve. But squashed circles and other irregular shapes can be Jordan curves too, just so long as their sides do not intersect each other and they are closed. A square is a Jordan curve. So is a rectangle.
Of the four images below, only the bottom left is a simple closed curve. The one beside it on the right is also closed, but it isn’t simple. The two on top are not closed.
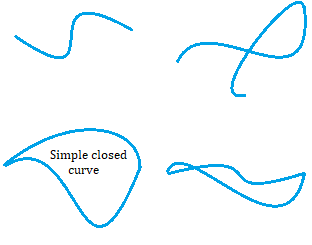
Properties of Simple Closed Curve
Jordan curves are topologically equivalent to a unit circle (a circle with a radius of 1). If you take any triangle T and a simple closed curve C, C will have an inscribed triangle similar to the triangle T.
References
Tverberg, Helge (1980), “A proof of the Jordan curve theorem” (PDF), Bulletin of the London Mathematical Society, 12 (1): 34–38, CiteSeerX 10.1.1.374.2903, doi:10.1112/blms/12.1.34. Retrieved from https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/blms/12.1.34 on August 18, 2019
Szabo, Tibor. Graph Theory– WS 06/07 Lecture Notes. Lecture 13, Turán-Type Problems, Planar Graphs I. Published Jan 24, 2007. Swiss Federal Institute of Technology, Zurich. Retrieved from https://www.ti.inf.ethz.ch/ew/courses/GT06/lectures/PDF/lecture13.pdf on August 18, 2019
Trident of Newton
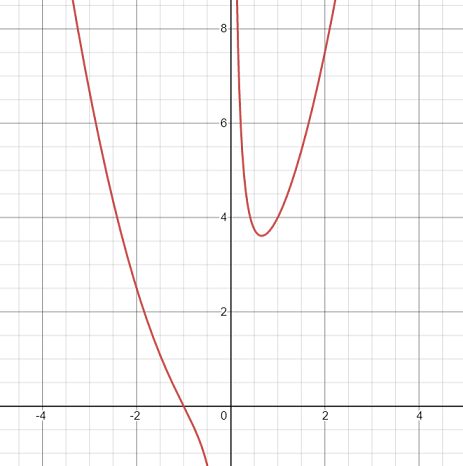
The Trident of Newton (or just “Trident”) is a cubic curve defined by the equation [1]
ax3 + bx2 + cx + d = xy,
where coefficients a, b, c, d, are real constants and a ≠ 0, ad ≠ 0.
The parametric equations and polar equations are, according to Dennis Lawrence [2], “not interesting.” The curve has one discontinuity at x = 0 and one asymptote at x = 0.
The curve, which is sometimes called a Cartesian parabola [3] or Parabola of Descartes (even though it isn’t a parabola) is an esoteric algebraic curve (“algebraic” means that it can be described with polynomials).
The above graph was created with Desmos. Click on the link and you’ll be able to specify different values for the constants.
History of The Trident of Newton
According to MacTutor [4], both Newton and Descartes studied the curve, although it was Newton who named it “trident.” The trident appears in Newton’s Introduction to the Quadrature of Curves. The text was translated into English by by John Harris in 1710 [5]. Newton states that the properties of the trident include:
- Four infinite legs (i.e., the four ends of the curve tend to infinity),
- Two tending towards contrary parts (i.e., the y-axis is an asymptote).
Other Meaning of Trident

As well as describing a plane curve, Newton used a trident symbol to describe Bismuth. Newton made creative and unorthodox use of alchemical symbols, most of which he created himself [6].
References
[1] Trident of Newton. Retrieved March 3, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/t/t328.htm
[2] Lawrence, D. (1972). A Catalog of Special Plane Curves. Dover Publications.
[3] Shikin, E. (2014). Handbook and Atlas of Curves. CRC Press.
[4] MacTutor. Trident of Newton. Retrieved March 3, 2022 from: https://mathshistory.st-andrews.ac.uk/Curves/Trident/#:~:text=The%20trident%20is%20the%2066,two%20tending%20towards%20contrary%20parts%20.
[5] Harris, J. (1710). INTRODUCTION TO THE QUADRATURE OF CURVES. London.
[6] Symbol Guide. Retrieved March 3, 2022 from: https://webapp1.dlib.indiana.edu/newton/reference/symbols.do