Butterfly Curve: Graphs, Equations

Quartic Curves >

There are two types of curve called the “Butterfly curve”:

1. Fay’s Parametric Curve,
2. Sextic Plane Curve.

Fay’s Butterfly Curve

The butterfly curve, discovered by Temple H. Fay in 1989 [1], is a transcendental curve with parametric equations [2]


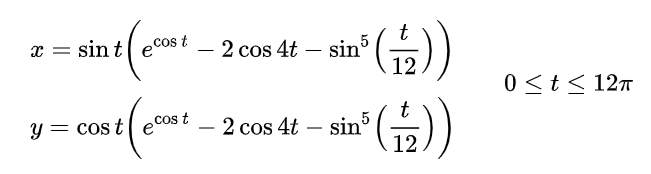
This video shows the butterfly curve:

Fay discovered the curve while investigating petal curves (not to be confused with pedal curves). The curve, according to Fay, is an example of a more complicated curve that “seems to spark interest and often brings surprises” and it “perhaps the most interesting and beautiful of all the curves” that the author discovered. The last term, sin⁵, was added purely for aesthetic appeal [1]. Various forms of the curve have been developed since Fay’s discovery, including a rotated butterfly curve [3]


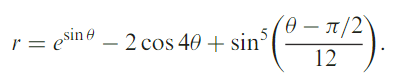
You can see Fay’s curve in action (and change the k-values for yourself) in this Desmos graph.
The butterfly curve can also be expressed in polar coordinates as:
ρ = e^cos(θ) – 2cos(4θ) + sin⁵(θ/12)
The formula describes a point’s trajectory as it traces the body of the butterfly. The variable ρ is the radial distance from the origin to the point. Variants can be obtained by lengthening the period of repetition, like
ρ = e^cos(θ) – 2.1cos(6θ) + sin⁷(θ/30) [4].

Butterfly Curve #2: Sextic Plane Curve

Another curve called the “butterfly curve” is a sextic plane curve given by the implicit equation [5]
y⁶ = (x² – x⁶)


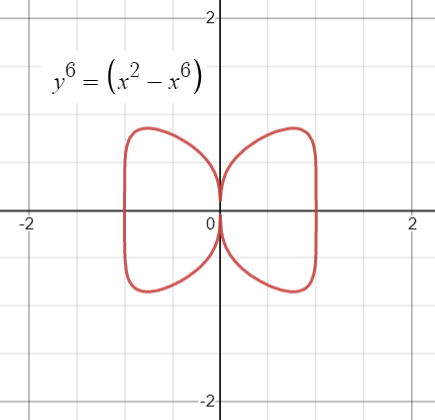
The area of both wings is given by the definite integral


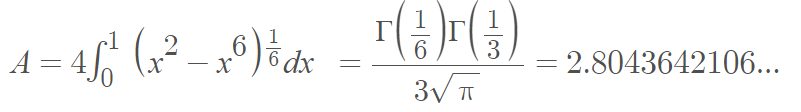
[6].

References

Butterfly animation drawn with: Desmos.com.
[1] T. Fay (American Mathematical Monthly, v96, n5 (May, 1989) :442 ). Retrieved January 15, 2022 from: https://www.jstor.org/stable/2325155?read-now=1&seq=1
[2] Young Hee Geum & Young Ik Kim. On the analysis and construction of the butterfly curve using Mathematica. July 2008International Journal of Mathematical Education 39(5):670-678 DOI:10.1080/00207390801923240
[3] Crumley, C. Parametric Curve Exploration.
[4] Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 72, 1989.
[5] Pickover, C. (2009). The Math Book. From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics.
[6] OEIS. Decimal expansion of (Gamma(1/6)*Gamma(1/3))/(3*sqrt(Pi)).