In calculus, “Normal” has a non-intuitive meaning. Normal within this context means perpendicular; a normal line to a point on a curve is a line that:
- Runs through the point and
- Is perpendicular to the tangent line.
The following image shows the normal line running through the curve and perpendicular to the tangent:
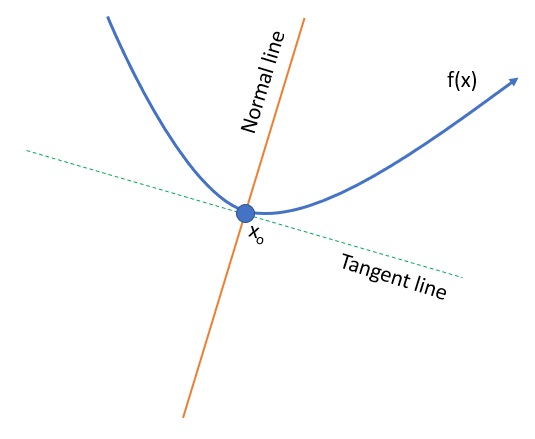
Since the normal line and tangent line are perpendicular, their slopes are opposite reciprocals. You can use the slope of the tangent line to find the slope of the normal line to the curve. For one-variable functions, a line through point (c,f(c)) is a tangent line if it has a slope of the derivative at that point, f′(c). The line is a normal line to f if it has a slope of −1/f′(c) [1].
The formula for the normal line is:
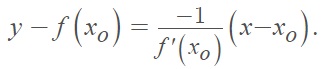
Where two lines are at right angles (perpendicular) to each other, the product of their slopes (m1·m2) must equal -1.
So, once you have the slope of the tangent line (i.e. the denominator in the above formula) you can figure out the slope of the normal line by taking the negative reciprocal (in other words, the two slopes, when multiplied together, should equal -1).
Another way to find the equation for the normal is to use the slope-point formula; It’s usually easier to define as you only need to find the slope and one point (x, y). This next example demonstrates the method.
Example: Finding the Equation for the Normal Line
Example Question: Find the equation of the normal line to the curve y = x√x at the point (1, 1).
Step 1: Find the derivative of the function (this gives us the slope of the tangent line).
The derivative of f(x) = x√x = xx½ = x3/2 can be found with the power rule:
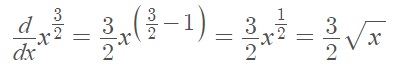
Step 2: Plug the given x-value into the derivative you calculated in Step 1.
The slope of the tangent when x = 1 is f′(1) = 3/2.
Step 3: Find the slope of the normal line. The slope is the negative reciprocal of 3/2, which equals -2/3.
The equation for the normal, in slope-point form (y – y1) = m(x – x1)), is:
y – 1 = -(2/3) (x – 1).
References
[1] 13.7 Tangent Lines, Normal Lines, and Tangent Planes. Retrieved July 15, 2021 from: https://sites.und.edu/timothy.prescott/apex/web/apex.Ch13.S7.html