Contents:
- The Plateau curve (of Joseph Plateau).
- Plateau of a curve (physics).
The Plateau Curve
The Plateau curve is also called the curve of Joseph Plateau, after the blind Belgian physicist who discovered that a curved wire frame dipped in a soap solution forms “beautiful curved surfaces” [1].
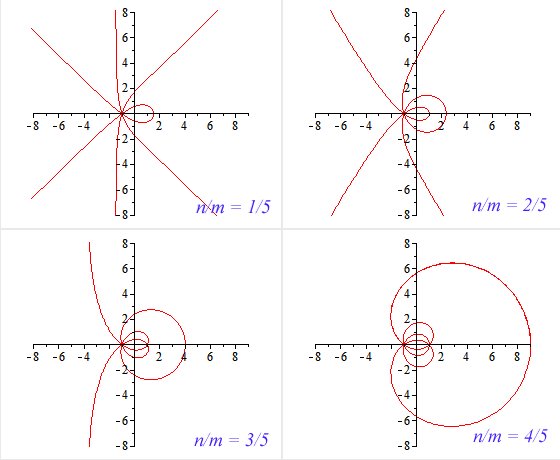
The Cartesian equation for the Plateau curve is:
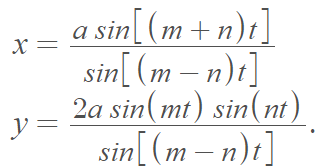
Where m ≠ n. If m = 2n, the curve degenerates to a circle centered at (1, 0) with radius 2 [2].
The Plateau of a Curve
A plateau curve (no capitalization) refers to a curve with a rapid rise, followed by a leveling off; the flat region that follows is called the plateau of the curve. Roughly speaking, curves with this form have the equation [3]
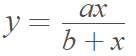
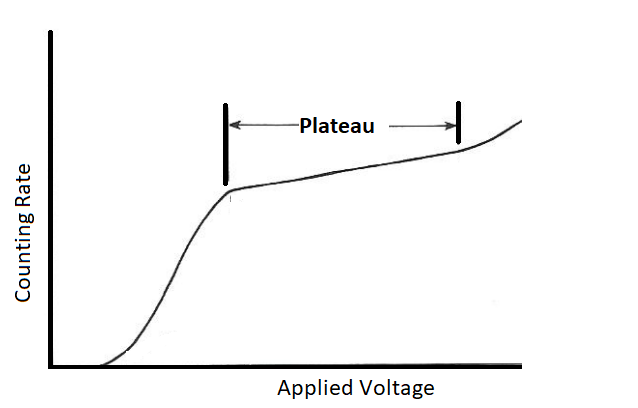
This type of curve has many uses in science and engineering. Plateau curves are often seen in models of high voltage, where they can help determine optimal input voltage [4]; The section of a Geiger Counter is characterized by the plateau curve [5]; there is a sharp ramp up when a Geiger tube turns on, followed by a plateau. In mechanics, the curve can model a flow curve of steady shear stress vs. shear-rate [6]. In biochemistry, the plateau curve models an enzyme-catalyzed reaction rate of a substrate as a function of the concentration of the substrate [7].
References
Image of curves: Hellingspaul,
[1] Britannica. Joseph Antoine Ferdinand Plateau. Retrieved February 24, 2022 from: https://www.britannica.com/biography/Joseph-Antoine-Ferdinand-Plateau
[2] Plateau Curves. Retrieved February 22, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/p/p351.htm
[3] Billo, E. (2007). Excel for Scientists and Engineers: Numerical Methods. Wiley & Sons.
[4] Lab 1 – Rough HV Plateau Curve. Retrieved February 24, 2022 from: http://atlas.physics.arizona.edu/~shupe/Physics_Courses/Phys_586_S2015_S2016_S2017/Lab%201%20write%20up%20Gia.pdf
[5] Lee, R. Plateau characteristics of Geiger Counters with respect to different gas mixtures and pressures. Masters Thesis. Retrieved February 24, 2022 from: https://scholarsmine.mst.edu/masters_theses/4836/
[6] Slippage and migration in Taylor–Couette flow of a model for dilute wormlike micellar solutions.