The term “smooth curve” has many meanings, depending on what field you’re working in. Unfortunately, it isn’t defined very well in calculus, with definitions varying from one text to another.
Informal Definition of Smooth Curve
Informally, a smooth curve is another name for a curve drawn smoothly, as opposed to jaggedly [1]. It describes a curve’s appearance, rather than any mathematical properties. For example, the following graph is smooth:
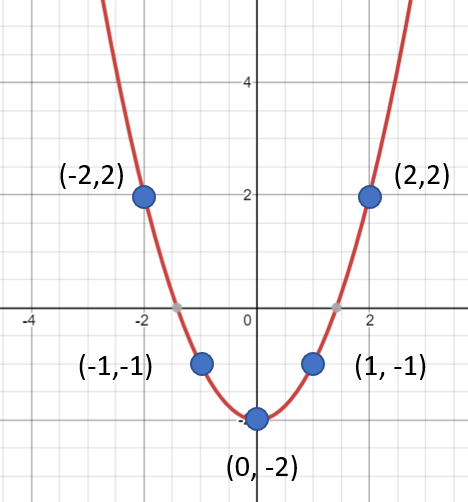
This one is not smooth:
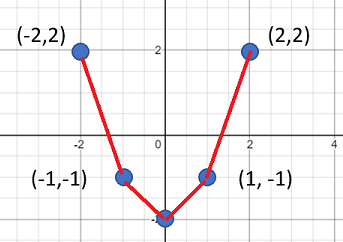
Smoothing in Statistics
In statistics, smooth curves (obtained through a process called smoothing) are produced by reducing noise in a dataset.
Smooth Curve in Calculus

In general, a smooth curve is a rectifiable curve created on an interval from a differentiable function. Unfortunately, definitions found in many elementary calculus textbooks are often slightly ambiguous [2].
For example, Larson & Edwards [3] definition is relatively simple, as the graph of a continuously differentiable, rectifiable function on an interval. Cochran et al [4] also make the link between rectifiable and smooth (p. 366). But Massani et al. [5] use the term in the informal sense (i.e. “draw a smooth curve”).
Smooth curves are sometimes defined a little more precisely, especially in numerical analysis and complex analysis. For example [6]:
A curve is smooth if every point has a neighbourhood where the curve is the graph of a differentiable function. A curve can fail to be smooth if:
- It intersects itself,
- Has a cusp.
References
[1] Clark. M. & Anfinson, X. (2012). Beginning and Intermediate Algebra: Connecting Concepts. Cengage Learning.
[2] Russell, E. & Sadek, J. (2005). A Note on the Definition of a Smooth Curve. Mathematics and Computer Education, v39 n1 p53-55
[3] Larson, R. & Edwards, B. (2016). Calculus, 10th Edition. Cengage Learning.
[4] Cochran, J. et al. (1987). Advanced Engineering Mathematics. Brooks/Cole Publishing Company.
[5] Massani, P. et al., (2014). Elementary Calculus. Elsevier Science.
[6] 1. Exercises from 3.2. Retrieved April 26, 2021 from: http://www.math.toronto.edu/~jmracek/Tutorial%2011.pdf