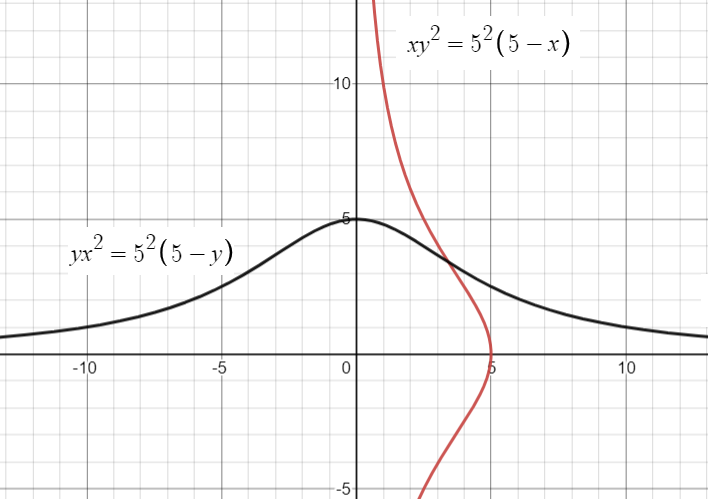
The Witch of Agnesi is a special case of a cubic hyperbola that is roughly bell-shaped.
The algebraic equation is
xy2 = a2(a – x).
Alternatively, the curve can be turned 90° so that it lies on the horizontal axis:
yx2 = a2(a – y).
The parametric equations are [1]:
- x(t) = at
- y(t) = a/(1 + t)2
The curve is named after the 18th century mathematician Maria Agnesi (1718 to 1799). It has a few surprising real life applications including as an approximation for the spectral line distribution of optical lines and x-rays. It also approximates the amount of power dissipated in resonant circuits [2].
Finding Derivatives
The coordinates x0 and y0 satisfy the equation
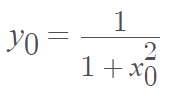
We can take the derivative (with the chain rule) to get:
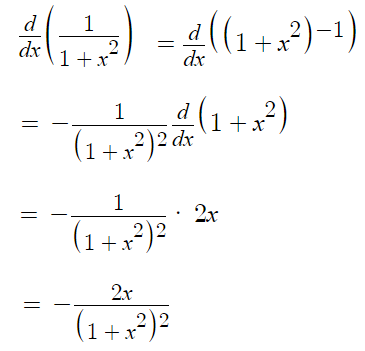
Construction of the Witch of Agnesi
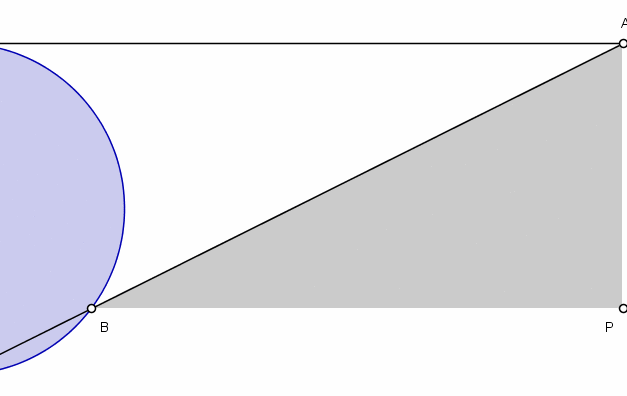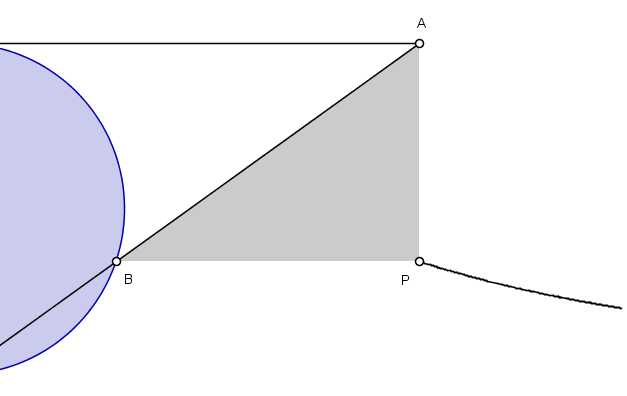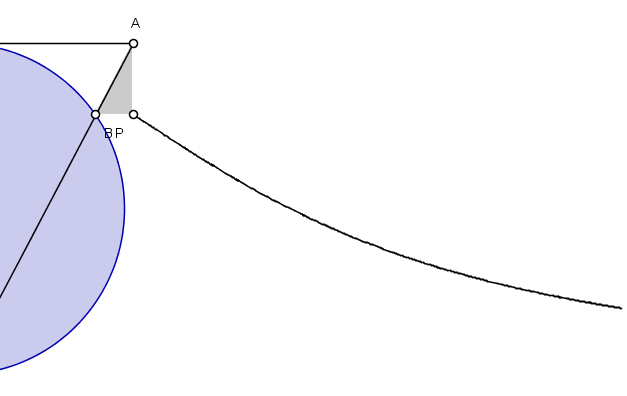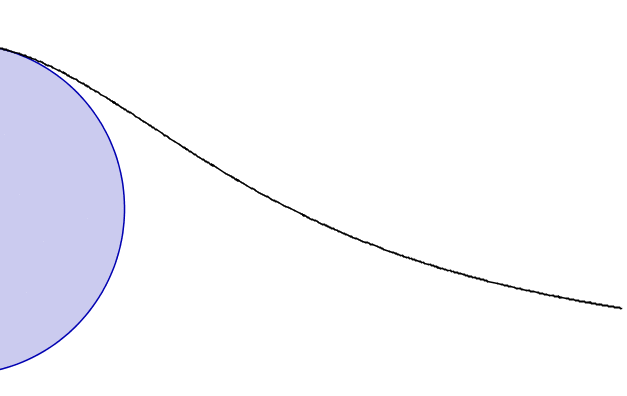
The curve can be constructed as follows [3]:
- Choose a circle of diameter a.
- Center the circle at (0, a/2)
- Choose a point A on the line y = a; draw a line from A to the origin. Mark a new point B where this line crosses the circle.
- If P is the point where the vertical line through P crosses the horizontal line through B, then the witch of Agnesi is the curve traced by P as A travels along the line y = a.
Why is it Called the Witch of Agnesi?
It turns out, it’s named the “witch” because of a mistake in translation [4]. Agnesi’s two-volume treatise on calculus included the curve, which she called versiera, which is Italian for “that-which-turns.” But when her work was translated into English by a Cambridge professor, he mistook the word for l’aversiera, which means “witch” in Italian.
References
[1] Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers.
[2] Applications to the Witch. Retrieved March 7, 2022 from: https://cs.appstate.edu/~sjg/wmm/final/agnesifinal/applications.pdf
[3] The Witch of Agnesi. Retrieved March 6, 2022 from: https://mathwomen.agnesscott.org/women/witch.htm
[4] Lienhard, J. No. 1741: THE WITCH OF AGNESI. Retrieved March 7, 2022 from: https://www.uh.edu/engines/epi1741.htm