An astroid curve (also called a tetracuspid, cubocycloid, or paracycle) is a special case of a hypocycloid with four cusps.
The Cartesian equation is [1]
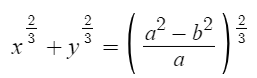
The parametric equation is
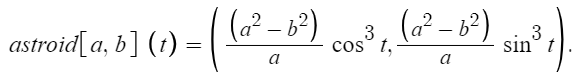
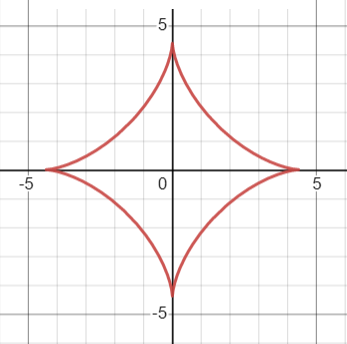
Hypocycloids are produced by tracing a fixed point on a small circle rolling inside the circumference of the larger circle. Cusps are meeting points for two branches of the curve with sharp corners and equal tangent lines.
Equation for the Tangent Line
We can use implicit differentiation to find an equation of the tangent lineat a given point [2].
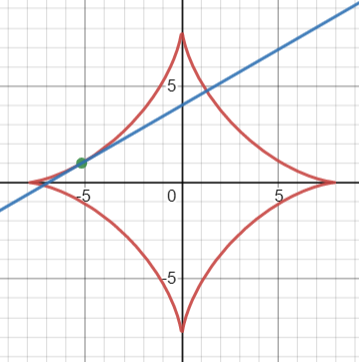
For example, to find the equation at (-3√3, 1):
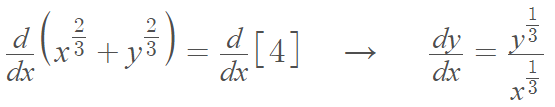
Substituting in (-3√3, 1) gives
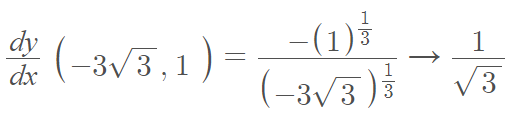
Finally, use the point-slope form of the equation for a line to get the solution
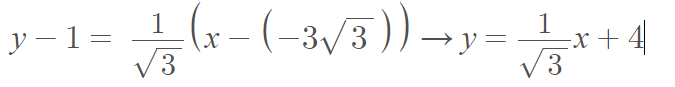
History of the Astroid Curve
The discovery of the curve is attributed to Roemer in 1674 [3], although it was formally named the astroid curve centuries later — in 1836. During that time the curve took on many names including the “four cusp curve.” The modern word asteroid (as in a small rocky body orbiting the sun) is derived from the name [4]. Sometimes the two words are confused, with some authors referring to the curve as the asteroid instead of the astroid. The curve has an important application in magnetism, where it is called the Stoner-Wohlfarth astroid.
References
Astroid graph created with Desmos.
[1] Tan, S. (2020). Handbook of Famous Plane Curves Using Mathematica.
[2] Stewart, J. Calculus, Early Transcendentals, p. 215, #30. Solution: https://sccollege.edu/Departments/MATH/Documents/Math%20180/03-05-030_Implicit_Differentiation.pdf
[3] O’Hanen, B. & Wisan, M. (2006). The Asteroid: Special Plane Curves/
Retrieved March 5, 2022 from: https://mse.redwoods.edu/darnold/math50c/CalcProj/sp06/mattben/RealWebsite/AsteroidPaper.html
[4] Silva, L. & Yokoyama, B. Final Project – The Astroid. Retrieved March 5, 2021 from: https://mse.redwoods.edu/darnold/math50c/CalcProj/sp07/breannelydia/Final.htm