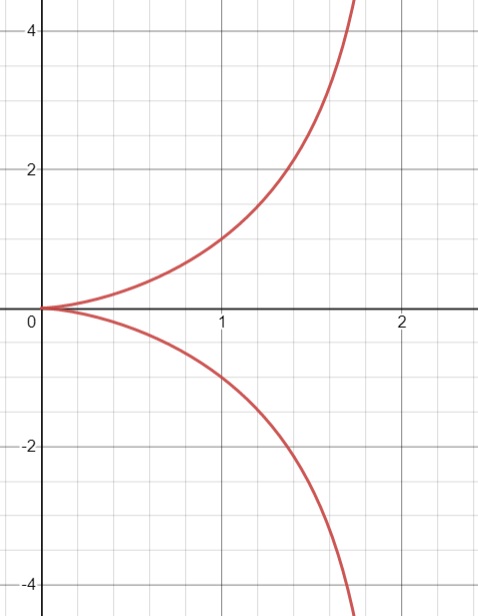
The Cissoid of Diocles (sometimes called “the” cissoid) is a pedal curve. A pedal curve is a curve formed by the feet of perpendiculars dropped from a moving point to a fixed curve. In the case of the Cissoid of Diocles, the moving point is the vertex of a parabola, and the fixed curve is a circle.
The Cissoid of Diocles is defined with the Cartesian equation
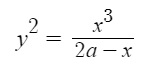
and the polar equation r = 2a tan θ sin θ.
The curve is named after Diocles , who originally studied the cissoid in about 180 BC to try and solve the classic problem of finding the length of the side of a cube with volume twice that of the given cube. This problem, called doubling the cube, involves two quantities a and b; you have to find x and y such that a, x, y, b are in geometric progression. “Doubling the cube” happens when b = 2a [1]; This result is not obvious though, so don’t be alarmed if you can’t connect the dots.
The name “cissoid” is found in the work of Geminus approximately 100 years later. Fermat and Roberval constructed the tangent in 1634; from any given point on the cissoid there are one or three tangents.
Construction of the Cissoid of Diocles
The cissoid of Diocles can be defined as the cissoid of a circle and a line tangent to it, with respect to the point on the circle opposite the point of tangency. Another way to define it: as the roulette of a parabola’s vertex as it rolls on an equally-sized parabola. These definitions might sound a little wordy, and if you’re not good with visualizations, they may not make a lot of sense to you. However, the construction of the cissoid is relatively simple[2]. For convenience, the unit circle is usually used [3]:
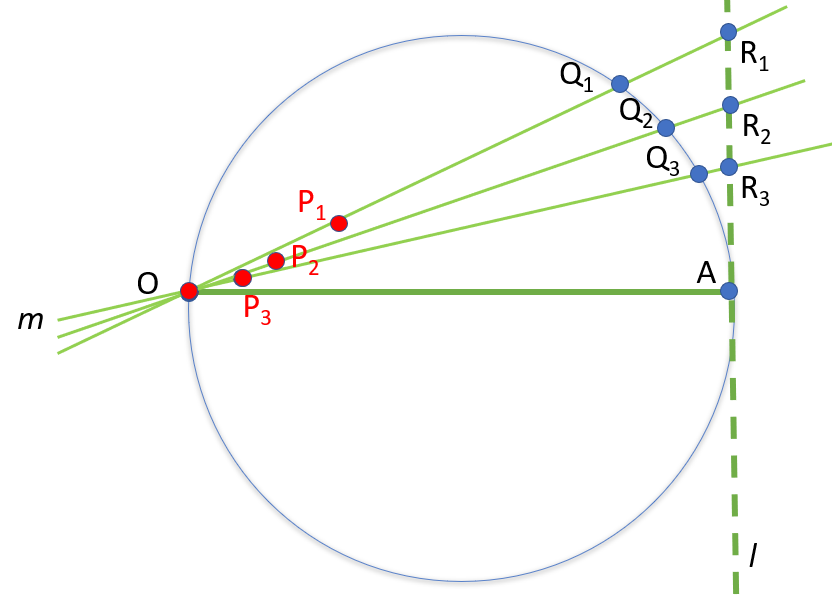
- Draw a circle C.
- Draw a diameter from O to A (these are the endpoints of the diameter).
- Sketch a tangent line l through point A.
- Draw a line through point O, cutting the circle (label this point Q), continuing the line through tangent line l (label this point R).
- Continue drawing lines through point O as in the above step. In the image, I’ve drawn three lines and three points P, which shows the beginnings of the cissoid shape. If you were to drawn many lines and many points (up to an infinite amount), the cissoid will take shape.
The cissoid is the set of points P (shown as red dots in the above image) for which OP = QR. It has a cusp (a phenomenon that first arises with cubic curves) at the pole O and is symmetric about an asymptote: the diameter of the circle (which is also the tangent line of the cusp).
A similar method is outlined in Stillwell’s Mathematics and Its History; it shows the symmetry of the curve [3]:
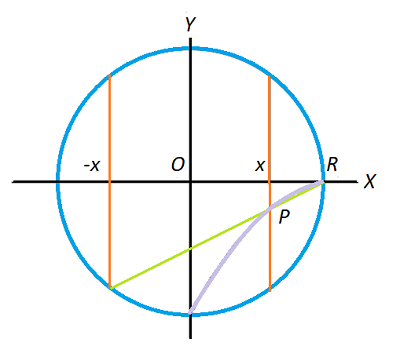
A portion of the curve is shown in the above image (from x = 0 to x = 1 on the unit circle. The two vertical lines (x and -x) show the symmetry of the Cartesian equation (y2(1 + x) = (1 – x)3); if (x, y) is a point on the curve, so is (x -y), In other words, you can drawn the complete curve by reflecting the result over the x-axis.
Interesting Properties and Applications
The Cissoid of Diocles has a number of interesting properties. It can be used to double the cube, which is a problem that was first posed by the ancient Greeks. It can also be used to construct a regular heptagon, which is a seven-sided polygon.
The Cissoid of Diocles has been used in a variety of applications, including architecture, engineering, and navigation. It is also a popular curve in mathematics, and it has been studied by mathematicians for centuries.
Some additional facts about the Cissoid of Diocles:
- The name “cissoid” comes from the Greek word “kissos,” which means “ivy.” The curve is named after the way that it resembles the tendrils of an ivy plant.
- The Cissoid of Diocles can be constructed using a compass and straightedge.
- The Cissoid of Diocles is a member of the conchoid family of curves.
- The Cissoid of Diocles can be used to generate the Fibonacci sequence.
References
Graph made with Demos.com
[1] The Cissoid. Retrieved January 18, 2022 from: http://math.fau.edu/yiu/CHP2015/CHP2015chapters32to36.pdf
[2] Kokoska, S. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers.
[3] Stillwell, J. Mathematics and Its History. 3rd Edition. Springer.