The Conchoid of Nicomedes, also called the Cochloid (Greek for “shell”), is a classic curve with two branches studied by the Greek mathematician Nicomedes around 200 BC [1]. Nicomedes used the construction to explore an ancient problem called doubling the cube; Pappus of Alexandria figured out that the conchoid of Nicomedes can be use to trisect an angle [2]. The curve, which was the first to solve the angle trisection problem, was a favorite of 17th century mathematicians [3]. Newton suggested the cochloid should be a “standard” curve [4].
In Cartesian coordinates, the conchoid can be written as
(x – a)2(x2 + y2) = b2x2
or alternatively,
(a – b – x)(a + b – x)x + (a – x)2y2 = 0.
In polar coordinates, the curve is r = a + b sec(θ)
The conchoid has one asymptote, at x = a.
The area between either branch and the asymptote is infinite. The area of the loop is
b√(a2 – b2) – 2ab log((a + √a2 – b2) / b) + a2cos-1(b / a)
The Conchoid of Nicomedes actually describes a family of curves— a different curve for each value of parameter a/
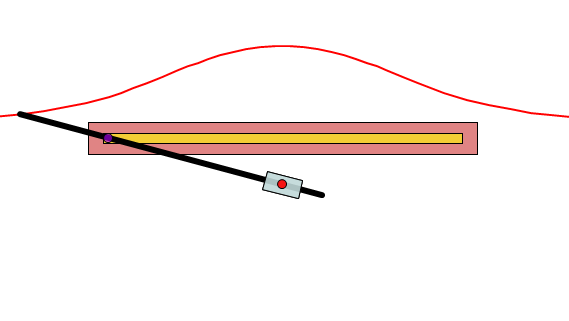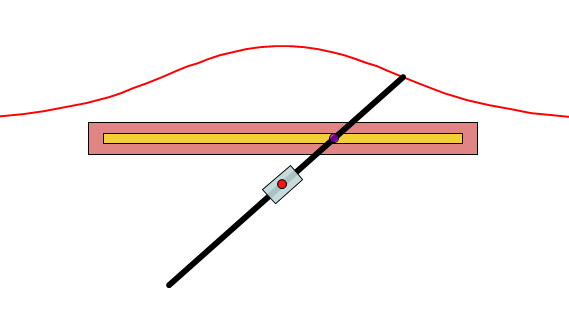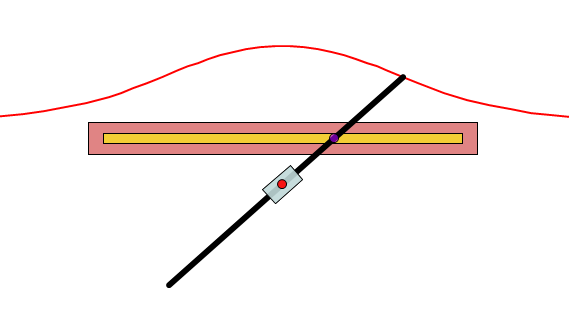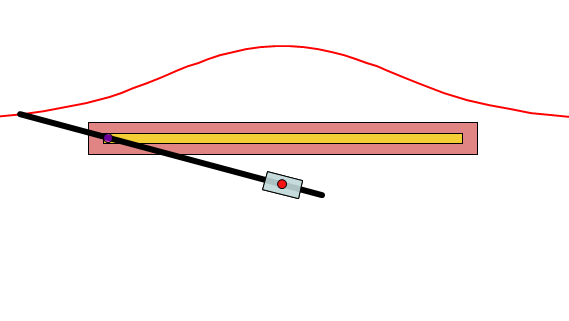
Construction of the Conchoid of Nicomedes
Nicomedes used a mechanical device to construct the device [5].
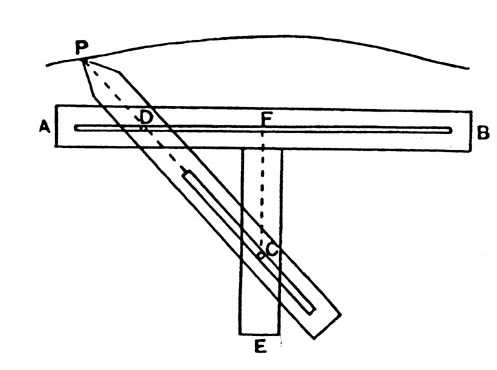
The above image shows a slotted ruler with length AB (called “the ruler” by Nicomedes). A second ruler, FE is fixed at right angles to the first ruler using a peg C. A third (also slotted) ruler PC pointed at P fits the peg C (this fixed point was called “the pole”). D is a fixed peg on PC in a straight line with the slot; it can move freely along the slot in AB. If then the ruler PC moves so that the peg D describes the length of the slot in AB on each side of F, the extremity P of the ruler describes the curve which is called a conchoid or cochloid. The constant length PD was called “the distance” by Nicomedes.
References
Top image: Philtodd,
[1] Knill, O. & Teodorescu, M. Conchoid of Nicomedes. Retrieved January 17, 2021 from: v
[2] Gardner, R. Chapter 4. Further Results in Euclidean Geometry. Retrieved January 17, 2022 from: https://faculty.etsu.edu/gardnerr/Geometry/notes-OW/Geometry-OW-4-1.pdf
[3] Jackter, A. The Problem of Angle Trisection in Antiquity. Retrieved January 17, 2021 from: https://sites.math.rutgers.edu/courses/436/436-s00/Papers2000/jackter.htmltm
[4] MacTutor: Curves (Conchoid). Retrieved January 17, 2021 from: https://mathshistory.st-andrews.ac.uk/Curves/Conchoid/
[5] Heath, Sir T. L., A History of Greek Mathematics. Vol. 1: From Thales to Euclid, Dover Publications, New York, 1981.