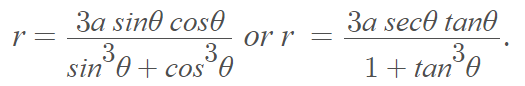The folium of Descartes (or noeud de ruban in French) is a single loop with one node (ordinary double point) and two asymptotes at the ends.
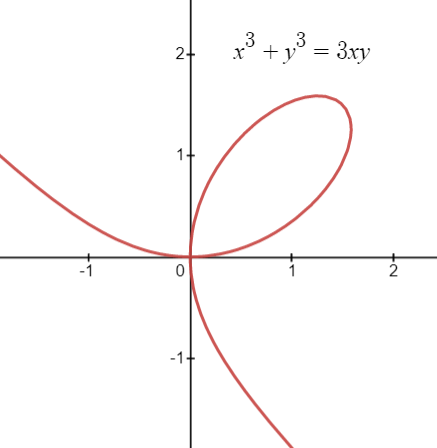
It is an algebraic curve defined by the equation x3 + y3 – 3axy = 0.
The curve can be graphed with parametric equations, as shown in this image:
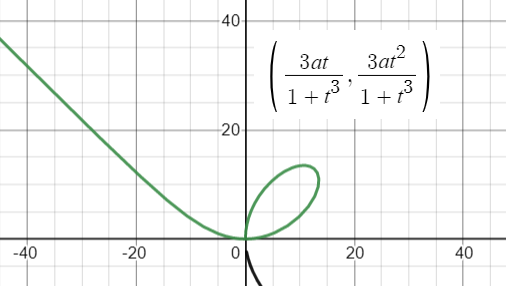
However, the parametric equations are not defined at t = -1. Therefore, you have to create a piecewise function graph that excludes t = 1 (In other words, graph two parts, one either side of t = 1).
Folium of Descartes Properties
- The curve is symmetric about the line y = x.
- One ordinary double point at the origin.
- Area of loop interior = 3a2/2.
- Area between asymptote and curve “wing” = 3a2/2.
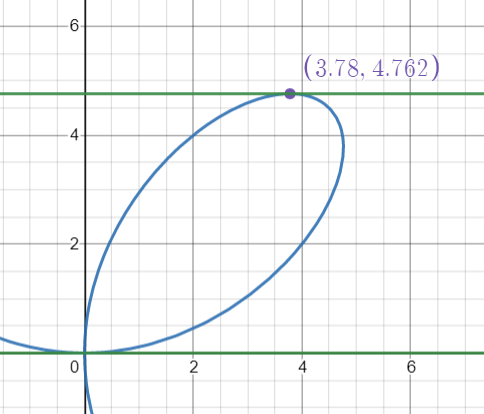
- Horizontal tangent lines at the origin and the point

The curve of Descartes is related to the trisectrix of Maclaurin by affine transformation.
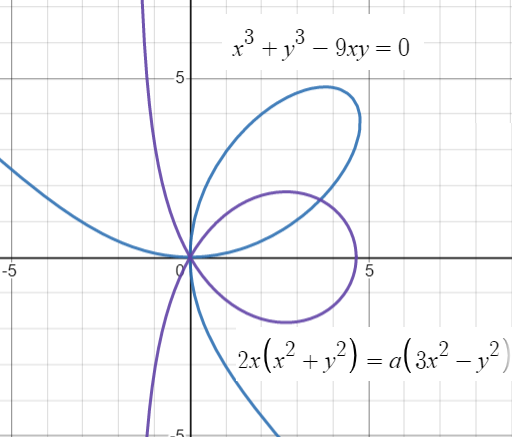
Finding Tangent Lines
Tangent lines for the curves can be found using implicit differentiation.
Example question: Find the tangent line for the point (2, 4) on Descartes folium.
Solution:
Step 1: Differentiate both sides of the equation with respect to x:
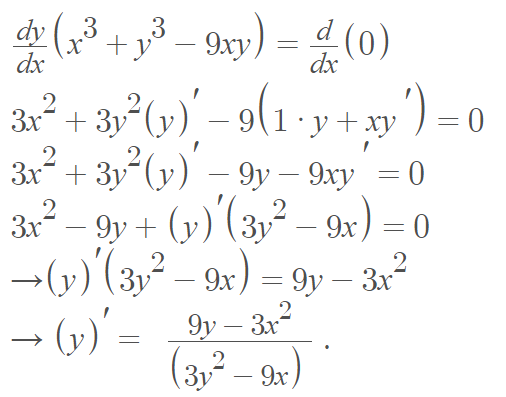
Step 2: Insert the coordinates (2, 4) into the formula and solve:
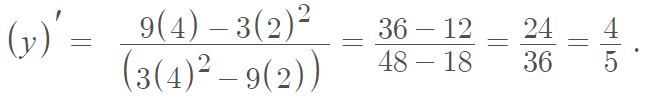
History of the Folium of Descartes
The folium of Descartes is named after René Descartes (1596 to 1650), who was the first to discuss it. He discovered the folium thanks to a challenge he put out to Fermat — to find a tangent line for an arbitrary point. While Fermat won the challenge, Descartes discovered his folium during the process [1].
The curve provided a role in the early development of calculus and provides the proof for some parts of Fermat’s Last Theorem [2].
Albania issued a postage stamp depicting Descartes and his folium in 1966 [1].

References
[1] Amoroso, R. FE, FI, FO, FOLIUM: A DISCOURSE ON DESCARTES’ MATHEMATICAL CURIOSITY from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.544.6091&rep=rep1&type=pdf
[2] Pricopie, S. & Udriste, C. Multiplicative group law on the folium of Descartes. Retrieved March 6, 2021 from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.402.4317&rep=rep1&type=pdf