Contents (Click to skip to that section):
- Line Segment Definition
- Directed Line Segment Definition
- Equivalent Directed Line Segments
- Endpoints
Problem Solving:
1. Line Segment Definition
Simply put, a line segment is just a piece of a given straight line. Each end of the line is called an endpoint. The two endpoints are usually denoted by letters, like A B or C D.
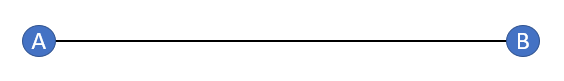
While AB is a common choice for endpoint labels, you could theoretically name them with any variable you like (e.g. FG or PQ). The usual notation is to write out the two endpoint labels with a line above them. For example: AB.
Directed Line Segment
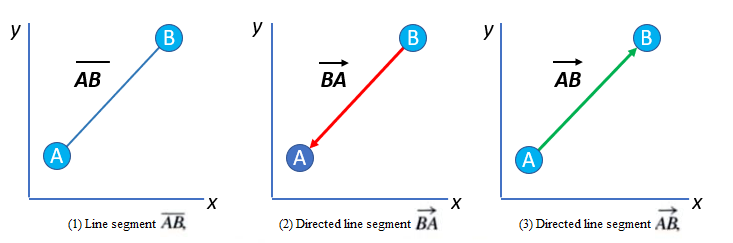
A directed line segment has, like the name suggests, a direction. The straight line is drawn with an arrow pointing in a definite direction. Many quantities, like acceleration, force, or velocity, involve a magnitude and a direction, so directed line segments, like lines (2) and (3) in the above image, are used to represent them. To put this another way, directed line segments are vectors (Kishan, 2007).
The initial point is where the line begins. In the above image, the initial points are point B (image 2) and point A (image 3). The terminal point is where the line ends: point A (image 2) and point B (image 3). The initial and terminal points are not interchangeable, so ![]() and
and ![]() are not the same.
are not the same.
2. Equivalent Directed Line Segments
Directed line segments are equivalent if they have the same length and direction. You can show that two segments are equivalent with the distance formula (an application of the Pythagorean theorem):
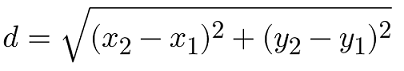
and slope formula (rise over run).
Example question: Are these two line segments equivalent?
- A(0, 0) to B(3, 2)
- C(1, 2) to D(4, 4).
Step 1: Apply the distance formula to both line segments (Note: the double lines || indicate length):
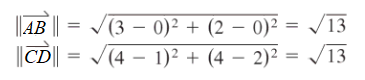
. Both segments are the same length (radic;13).
Step 2: Use the slope formula for both segments:
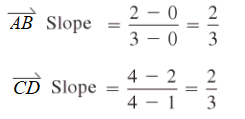
Both segments have the same slope.
The two line segments have the same length and slope, so they are equivalent.
3. Endpoints
An endpoint is a point at the boundary of one end of a closed interval, ray, or line segment. It’s literally the point where the interval, ray, or line ends.
Endpoint on a Ray and Line Segment
A ray only extends indefinitely in just one direction. A ray is denoted with an arrow above the two endpoints. The initial point is where the line is limited (i.e. ends abruptly) and the terminal point is where the ray continues indefinitely. In ray notation, an arrow is placed above the two endpoints; the initial point comes first.
For example, the following image shows the ray ![]() :
:


Use of Endpoints
Endpoints are primarily used to find Riemann sums. The right-hand rule uses right endpoints for the calculation; The left-hand rule uses left endpoints.
The term is also used define points where a function simply ends.
An important note though, is that an endpoint in calculus isn’t usually a “point” in the usual sense of the word. It’s defined by a directional derivative or limit (i.e. values leading up to the endpoint, rather than the value at the endpoint itself).
Problem Solving: Length of a Line Segment & The Distance Formula
The length of a line segment between two points is calculated with the distance formula:
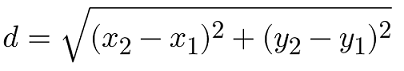
This formula only works for linear (straight line) functions. If you have a curved function, use the arc length formula instead.
Length of a Line Segment: Example
Example question: What is the length of the line segment for f(x) = 5x + 2 on the interval [0,1]?
Step 1: (Optional) Draw a Graph of the function. This step can help you see where the points you need for the formula are (x1, x2, y1, y2). I used Desmos.com to create this graph:
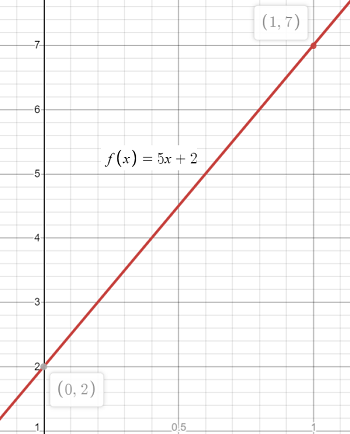
A quick look at the line segment between these two points and I’m going to guess that the length should be around 5. That gives me a way to check that my final answer is reasonable.
Step 2: Plug your two (x, y) coordinates into the distance formula.
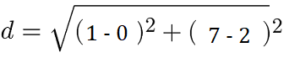
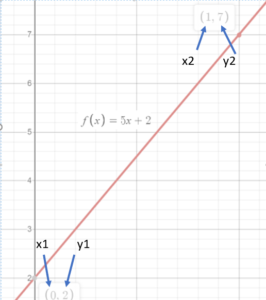
If you’re having trouble deciding which point goes where, the following graph has the x and y points labeled.
Step 3: Simplify and solve:
- (1 – 0)2 = 1
- (7 – 2)2 = 25
- 1 + 25 = 26
- √(26) ≈ 5.1
So my guess at 5 was fairly close.
Length of a Line Segment & Pythagorean Theorem
You might notice that the distance formula is really an application of the Pythagorean theorem. And in fact, you could get to the same answer by using the Pythagorean formula a2 + b2 = c2.
The following image shows that the hypotenuse of the triangle lies on the line segment you’re trying to find the length of:
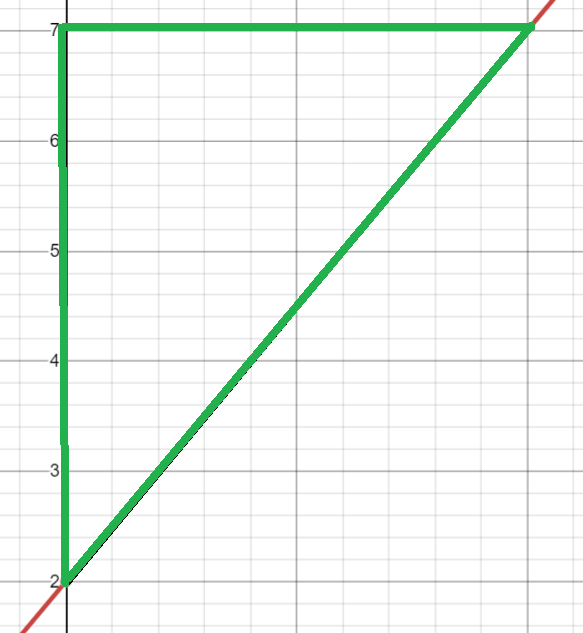
You may be wondering why we use the distance formula to find the length of a line segment instead of the more simple Pythagorean formula. The answer is that while a, b, and c work perfectly well in geometry, it doesn’t translate well to the Euclidean plane of x’s and y’s, especially once you get to variations on the distance formula for curves. You can’t fit a triangle to a curve, but you can fit a series of small lines. This process of fitting small lines to approximate a curve uses integration, and (along with derivatives) it’s one of the two fundamental areas of calculus.
References
Introduction to Geometry: Rays and Angles
Deriving the Arc Length formula
Contents:
An “arc” is a curve segment; The arc length tells you how long this segment is.
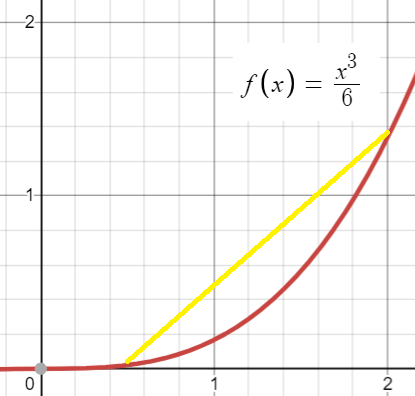
Formal Definition of Arc Length
In calculus, the arc length is an approximated with straight line segments using a definite integral variation of the distance formula.
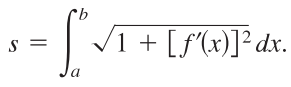
Where:
- s is the arc length,
- a, b are the integral bounds representing the closed interval [a, b],
- f′ is the first derivative.
Arc Length Formula Example
Although the formula uses line segments, it’s wrapped up in the integral equation, so you’ll be using that instead of the line segment formula.
Example Question: Find the arc length of f(x) = x2/8 − ln(x) on the interval [1,2].
Step 1: Find the first derivative of the function. This solution uses the power rule and the derivative for natural log rule:
f′(x) = (x/4) – (1/x).
Step 2: Insert the derivative into the arc length formula. Don’t forget to add the integral bounds:
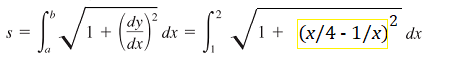
Step 3: Evaluate the integral, using the usual methods of integration or an online integral calculator (I used the one at integral-calculator.com).
Arc length = ln(2) + (3/8) ≈ 1.068.
Notes on The Challenging Arc Length Formula
Unfortunately, many of the definite integrals required to calculate arc length are extremely challenging or even impossible to compute [1, 2]. You may want to use a calculator, like I did in the example above, to avoid the frustration of dealing with impossible-to-solve integrals, which happen a lot for the arc length formula.
For example, look at what happens to the following fairly basic function:
Example question: Find the arc length of f(x) = x3/6 between ½ and 2.
Step 1: Find the first derivative of the function (this example uses the power rule):
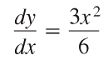
Step 2: Insert the derivative into the formula for arc length:
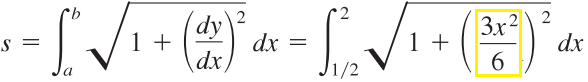
Simplifying:
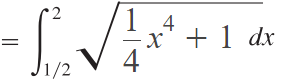
Step 3: Evaluate the Integral. At this point, the integral is impossible to evaluate using the “usual” methods of integration. Which means that we have to use other methods to approximate the arc length.
Rectifiable Curve: Finite Arc Length
A rectifiable curve has a finite arc length. It can be approximated with a series of line segments.
Nonrectifiable curves, like fractals, have infinite length. They could also be called curves that are rectifiable by straight lines; their arc lengths can be expressed as elementary functions of their endpoints [3]. Many basic curves are rectifiable, including cycloids. Non-rectifiable curves include the Koch snowflake, circle and ellipse.

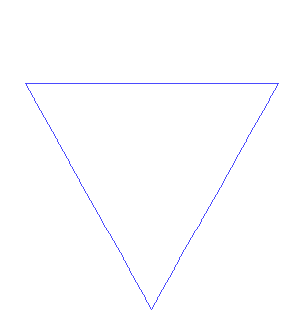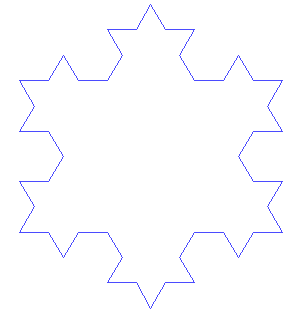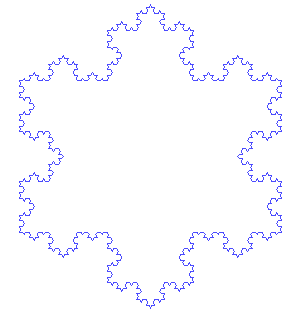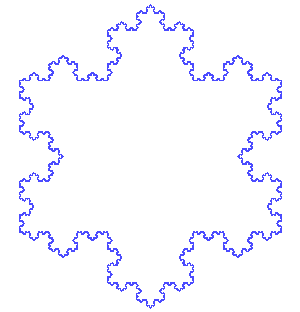
Defining a Rectifiable Curve
Formally, we can define a rectifiable curve as follows:
If a first derivative for a function is a continuous function on the closed interval [a, b], the graph is rectifiable between (a, f(a)) and (b, f(b)). Functions that meet this criteria are continuously differentiable on the specified closed interval and have a smooth curve between the two points [4].
Dealing With Nonrectifiable Curves
In calculus and real analysis, we’re mostly interested in rectifiable curves of finite length as they are straightforward to analyze. In a way, calculus can “force” a curve to be rectifiable: it’s length can be measured by very small line segments, leading to extremely accurate “approximations.”
The humble parabola is nonrectifiable, but we normally only deal with intervals of a parabola in calculus; In the rare case when you want to analyze a parabola over its entire (infinite) length, it can be made rectifiable by adding or subtracting its arc length to the length of an auxiliary parabola [3]. Nonrectifiable curves can also have their arc lengths expressed in terms of transcendental functions. Nonrectifiable curves also show as solutions to half-linear differential systems [5].
Arc length distribution
The arc length distribution considers the random uniform placement of a finite number of arcs on a space such as the unit circle, where the arc lengths are sampled from a probability distribution such as the uniform distribution.
Arc Length / Line Segment References
[1] Edwards, B. & Larson, R. (2009). Calculus, 9th edition. Cengage Learning.
[2] 9.9 Arc Length. Retrieved April 12, 2021.
[3] Moll, V. et al. (2002). Bernoulli on arc length.
[4] Larson, R. & Edwards, B. (2009). Calculus, 9th Edition. Cengage Learning.
[5] Naito, Y. et al. (2018). Rectifiable and Nonrectifiable Solution Curves of Half-Linear Differential Systems. Math. Slovaca 68. No 3. 575-590. Retrieved April 11, 2021 from: https://search.proquest.com/openview/60993ad5055fb6bd783b70fcb571d77d/1?pq-origsite=gscholar&cbl=2038886
Cycloid image: Zorgit, CC BY-SA 3.0