Kampyle of Eudoxus

Quartic Curves >

Kampyle of Eudoxus is a family of curves studied by the Greek mathematician Eudoxus in relation to doubling the cube; Eudoxus, a student of Plato, was famous for finding formulas for measuring cones, and cylinders, and pyramids [1]. He also constructed the first mathematical model of the universe [2].

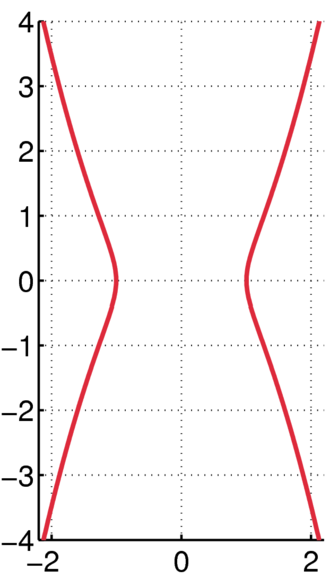
The word kamplye (pronounced with three syllables) comes from the Greek word for “crooked staff” [3].

The general formula for kampyle of Eudoxus is:

a²x⁴ = b⁴(x² + y²)

Where:

• a and b are nonzero constants,
• (x, y) ≠ (0, 0). In other words, the origin is excluded as a solution to the equation.

This is an open curve that never closes or completes. It is an increasing curve—single, non-repeating curvature [4].

The curve has the polar equation r cos² θ = a.
The parametric equations are x = a sec(t); y = a tan(t) sec(t), where t ∈ [-π/2, π/2]. The curve has discontinuities at t = ± π/2 [2].

Derivative of Kampyle of Eudoxus

The derivative of the curve can be found with implicit differentiation:

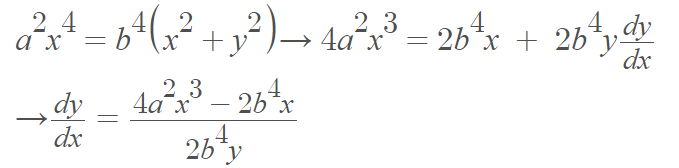
Geometry of Kampyle of Eudoxus

• The two intercepts are: (0, a, 0), (π, -a, 0).
• The minimum is at (0, a, 0).
• The maximum is at (π, -a, 0).
• There are four points of inflection: (tan^-1 ± (√2)/2, ± a(√6)/2, a(√3)/2 [5].

References

[1] Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers.
[2] Tan, S. (2020). Handbook of Famous Plane Curves Using Mathematica.
[3] Schwartzman, S. (1994). The Words of Mathematics. An Etymological Dictionary of Mathematical Terms Used in English. Mathematical Association of America.
[4] Krawczyk, R. Seashell Interpretation in Architectural Forms.
[5] Lawrence, J. (2013). A Catalog of Special Plane Curves. Dover Publications.