Rhodonea Curve (Rose Curve)

Plane Curves >

A Rhodonea curve (also called a rosette, rosace, roseate curve or rose curve) is a plane curve shaped like a petalled flower.

Equations for the Rhodonea curve

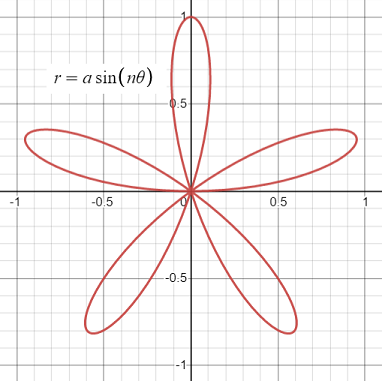
The rhodonea curve is a sinusoid (a curve with the form of a sine wave) with the polar equation

r = a sin(nθ), or
r = a cos(nθ)

The two variants differ by a rotation of π/2.

• The variable a controls the amplitude of the function; graphically, it controls how far from r = 0 the curve extends outwards. For example, r = 4*sin(4θ) means that the curve extends to y = 4.
• The variable n controls the number of petals [1]:
  • Odd n = n-petalled.
  • Even n = 2n-petalled,
  • Irrational n = infinite petals.
• The independent variable, θ, is the angle;
• The dependent variable, r, is the radius as a function of θ.

The Cartesian equation is a lot less intuitive and a lot more complex. For example, the four petal quadrifolium (Rosace a quatre jeulles), has the polar equation r = a sin 2θ or the Cartesian equation (x² + y² = 4a²x²y² [2].

You can play around with the various values using this Desmos graph.

The curve can also be described by a pendulum in a plane orthogonal to its rotating axis, as n is large [3].

There is an interesting connection between the rhodonea curve and first kind Chebyshev polynomials; the polar equation for the rhodonea curve can be interpreted as T_n(cosθ), which is the definition of Chebyshev polynomials of the first kind [4].

History of the Rhodonea Curve

Luigi Guido Grandi (1671 to 1742), a mathematics professor at the University of Pisa, Italy, studied the curve in the 1700s and named it the rhodonea curve, which translates to “rose” [5].

References

[1] Rose. Retrieved February 25, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/r/r382.htm
[2] Smith, D. (1958). History of Mathematics, Vol. II. Dover Publications.
[3] Pons, O. (2015). Analysis And Differential Equations. World Scientific Publishing.
[4] Integral Transforms and Operational Calculus.
[5] The Rose Curve. Retrieved February 25, 2021 from: https://mse.redwoods.edu/darnold/math50c/CalcProj/sp07/hanskatie/therose.ppt