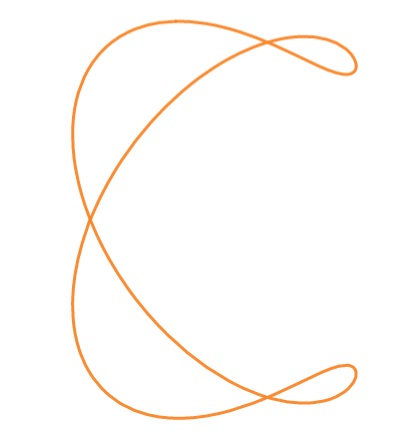
The ampersand curve, which resembles an ampersand “&”, is a quartic curve with the algebraic equation:
6x4 + 4y4 – 21x3 + 6x2y2 + 19x2 – 11xy2 – 3y2 = 0.
Alternatively, the implicit equation is [1]:
(y2 – x2)(x – 1)(2x – 3) = 4(x2 + y2 – 2x)2.
The curve has three ordinary double points in the real plane at (x, y) = (0, 0), (1, 1) and (1, -1) [2].
History of the Ampersand Curve
The named “ampersand curve” was popularized by Cundy and Rollett [3], but they weren’t the first to study it. According to John Derbyshire, author of Unknown Quantity: A Real and Imaginary History of Algebra [4], the curve can be found in a 19th century book by Percival Frost called An Elementary Treatise on Curve Tracing which was published in 1892 and showed the reader a myriad of methods for turning algebraic equations into drawn curves. The ampersand figure can be found in Frost’s book as Plate VII, Figure 27.
The ampersand curve is sometimes called the Plücker quartic, after J. Plücker who constructed a version of the ampersoid in his Theorie der algebraischen Curven [5].
References
[1] Knill, O. Curves.
[2] Bobenko, A. (Ed.). (2011). Computational Approach to Riemann Surfaces. Springer.
[3] H.M. Cundy, A.P. Rollet, mathematical models, Oxford, Clarendon Press (1972), traduit en français : modèles mathématiques, Cédic (1978).
[4] Derbyshire, J. (2006). Unknown Quantity: A Real and Imaginary History of Algebra. Joseph Henry Press.
[5] Plücker, J. Theorie der algebraischen Curven: Gegründet auf eine neue Behandlungsweise der analytischen Geometrie. Berlin: Adolph Marcus, 1839.