A hippopede is a closed curve with the polar equation [1]
r2 = 4b(a – bsin2θ).
Or, alternatively by the implicit equation
(x2 + y2)2 = cx2 + dy2.
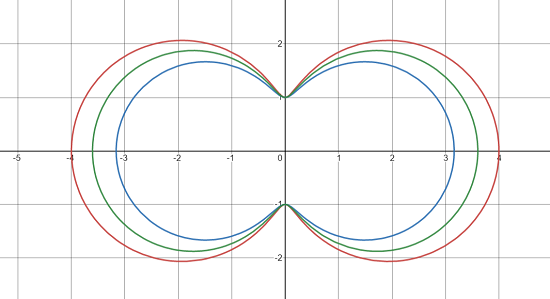
When d > 0, the curve becomes an oval and is called an Oval of Booth. When d < 0, the curves resembles a figure and is sometimes called the lemniscate of Booth. When d = -c, the hippopede is equivalent to the lemniscate of Bernoulli.
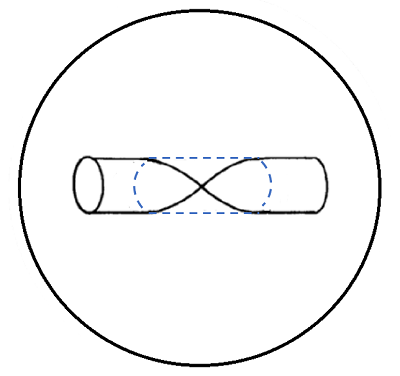
In three dimensions, the hippopede is the intersection of a cylinder and a sphere; you can think of it as a figure 8 drawn on a sphere [2]. The cylinder pierces the sphere; from the inside, the cylinder is tangent to the sphere.
History of the Hippopede
The Greek mathematician Eudoxus of Cnidus (40 to 355 BC) made the earliest known attempt to model planetary motion; he invented a scheme of nested concentric spheres; when a planet attached to both spheres rotated around different axes in opposite directions, it would trace out a hippopede retrograde motion. Eudoxus’s hippopedes were fixed in size and shape, so if you changed the parameters to match a planet’s speed during retrograde, you couldn’t match its arc (or vice versa) [3].
The hippopede is also called a horse fetter, because it looks like the loop of ropes used for restraining a horse’s feet (alternatively, a horse fetter is a training exercise to keep a horse from leaning in one direction). It was Eudoxus who gave the curve the name hippopede; horse fetters were a favorite practice in riding schools in ancient Greece [4]. It’s uncertain though, whether Eudoxus named the shape after the riding practice or the tethering device.
References
Curves created with Desmos.com.
[1] Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 144-146, 1972.
[2] Neugebauer, O. (2012). A History of Ancient Mathematical Astronomy. Springer Berlin Heidelberg.
[3] To Save the Phenomena.
[4] Dreyer, J. (1906). History of the Planetary Systems from Thales to KEpler..