A spiric section (also called the spiric of Perseus), is a quartic plane curve defined by the equation
(x2 + y2)2 = dx2 + ey2 + f.
As polar coordinates:
(r2 – a2 + b2 + c2)2 = 4b2(r2 cos2 θ + c2)
or
r4 = dr2 cos2θ + er2sin2θ + f.
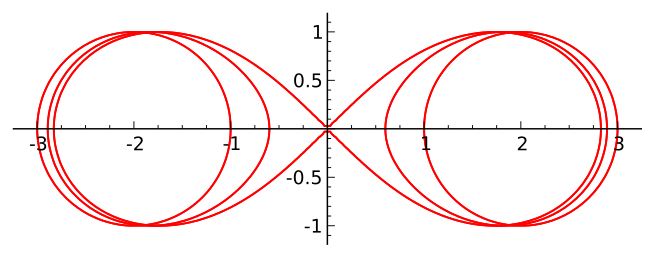
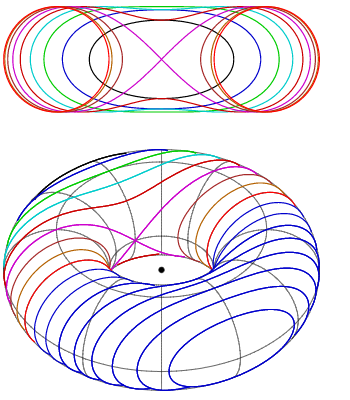
They can also be defined as bicircular curves that are symmetric to both the x-axes and y-axes. Alternatively, as the curve that results from the intersection of a torus and a plane, parallel to its rotational symmetry axis. However, this particular definition doesn’t specifically include the curves produced by imaginary planes [1]. A spiric section that has a plane at distance r from the axis is called an oval of Cassini [2].
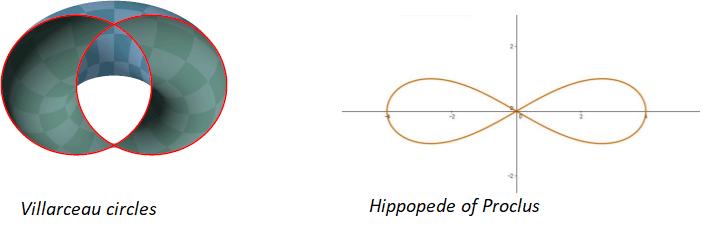
Spiric sections are a member of the family of toric sections, and they can take on a wide variety of different shapes, including being interlaced like a horse’s hobble or fetter, broad in the middle and thin at the sides, or elongated with a narrow middle portion and broad ends [3]. Named members include Bernoulli’s lemniscate (which was the key to unlocking the secretes of elliptic integrals), the Cassini ovals, the Hippopedes of Proclus, and Villarceau’s circles. Cassini’s ovals are spiric sections (which are hippopedes) where the distance of the cutting plane to the torus axis is equal to the generating circle’s radius; Bernoulli’s lemniscate is a special case of a Cassini’s oval, generated when R = 2r [4].
Spiric Section History
Bicircular curves were known to the ancient Greeks long before the spiric sections were studied. One of them is the Conchoid of Nicomedes, invented before 200 BC [7]. However, The earliest source of this type of curve is attributed to Eudoxus of Cnidus (40 – 355 BC), whose work on planetary movement centers on the hippopede, which isn’t a plane curve but a curve on a sphere. Menaechmus (380 to 320 BC) constructed conic sections, by cutting a cone with a plane.
Two centuries later, Perseus (2nd BC) studied the spiric section by cutting a torus with a plane (giving it the name “spiric of Perseus”) [2], parallel to the line through the center of the torus’ hole [1] (a hole is a topological structure that prevents a mathematical object from being continuously shrunk to a point) [5]. Although Perseus’s work is lost to history, and practically nothing in known about him, we do know of his research through obscure commentaries [6]. For example, Proclus (411 to 485) wrote that “a mathematician known as Perseus considered the intersection of a torus and a plane which is parallel to the equatorial plane of the torus” [7].
The spiric section was rediscovered in the 17th century, when mathematicians, including Cassini) were studying quartic curves. Interestingly, Cassini (1625–
1712) was a distinguished astronomer but opposed Newton’s theory, rejected Kepler’s ellipses and instead proposed his own Cassini ovals as models for planetary orbits [8].
Use of Spiric Sections
Spiric sections have some important uses, beyond their study in geometry. For example, in quantum mechanics, the Double Quantum Dot (DQD) structures potential cross-section can be approximated by a spiric section [9].
References
Images:
Top spiric section: Ag2gaeh,
Krishnavedala,
[1] Dayanithi, C. Combination of Cubic and Quartic Plane Curve. IOSR Journal of Mathematics (IOSR-JM). e-ISSN: 2278-5728,p-ISSN: 2319-765X, Volume 6, Issue 2 (Mar. – Apr. 2013), PP 43-53 www.iosrjournals.org.
[2] Coffman, A. The Hippopede of Proclus.
[3] Proclus. (2020). A Commentary on the First Book of Euclid’s Elements. Princeton University Press.
[4] Marconi, L. The toric sections: a simple introduction. Retrieved January 20, 2022 from: https://arxiv.org/pdf/1708.00803.pdf
[5] Weisstein, E. (1999). Hole. Retrieved January 20, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/h/h318.htm
[6] Horadam, F. (2014). Outline Course of Pure Mathematics. Elsevier Science.
[7] Werner, T. (2011). Dissertation. Rational families of circles and bicircular quartics. Der Naturwissenschaftlichen Fakult at der Friedrich-Alexander-Universit at Erlangen-Nurnberg zur Erlangung des Doktorgrades Dr. rer. nat.
[8] Stillwell, J. Mathematics and Its History. 3rd Edition. Springer.
[9] Foundations of Quantum Mechanics In The Light Of New Technology: Isqm-tokyo ’08 – Proceedings Of The 9th International Symposium. 2009. World Scientific Publishing Company.