A cusp or corner in a graph is a sharp turning point. These are critical points: either a local maximum (the tallest point on the graph) or local minimum (the lowest point).
Cusps in Graphs: Examples
In general, the easiest way to find cusps in graphs is to graph the function with a graphing calculator.
Example: The function f(x) = x2/3 has a cusp at x = 0. This is shown on the following graph:
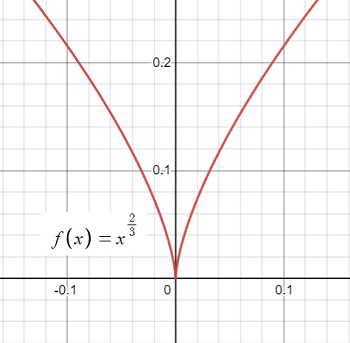
The first derivative is undefined at x = 0 because of division by zero:
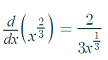
Example #2: The graph of f(x) = |x2 – 4| has two cusps: one at x = 2 and one at x = -2:
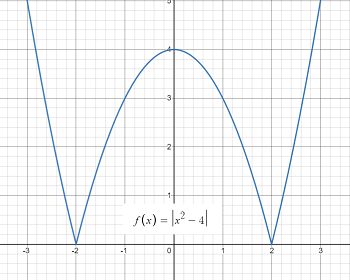
The function isn’t differentiable at those critical points because of division by zero:
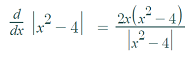
Corners work the same way: they are sharp turns:
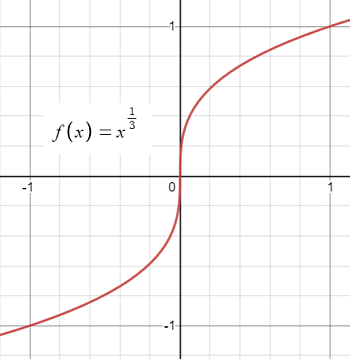
Why are Functions with Cusps and Corners not Differentiable?
A function is not differentiable if it has a cusp or sharp corner. As well as the problems with division by zero shown above, we can’t even find limits near the cusp or corner because the slope to the left of the cusp is different than the slope to the right.
For example, the following graph shows f(x) = x2/3 and its derivative near the cusp:
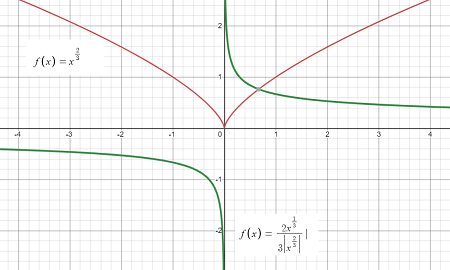
As you approach x = 0 (the place where the cusp is) from the left, the derivative (green graph) has a different value from what you get if you approach x = 0 from the right.
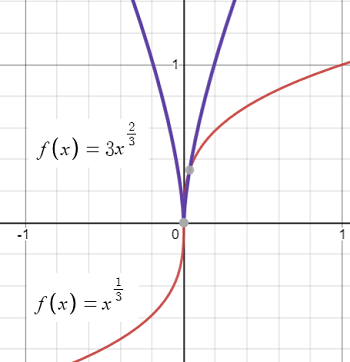
Corners have the same problems: approaching from the left or from the right gives you different values for the derivative. The following graph shows a corner (a vertical tangent) for the function f(x) = x1/3 and it’s derivative (blue graph).
References
Desmos.com graphing calculator (images).