A hyperbola is an open curve with two opposite, mirror-image parabolas.
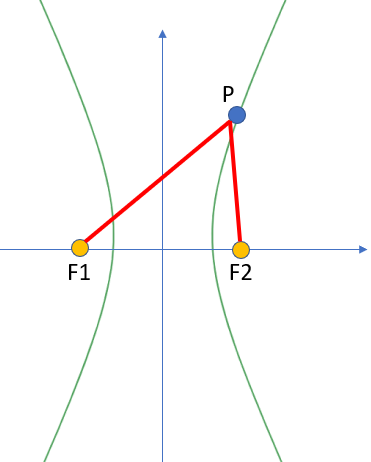
More formally, it is a collection of points in the plane where the absolute value of the difference of the distances from a point on the hyperbola to each foci is a fixed constant. Another way to put this: point P on the curve shown above is always closer to F2 than F1 by a fixed amount. If point P were on the left-hand curve (instead of the right), then point P would always be closer to F1 than F2 by the same fixed amount. As a formula:
|P(F1) – P(F2)| = constant.
Parts of a hyperbola:
- The branches are the two continuous curves.
- The two lines connected the focal points F1 and F2 are the focal radii at point P.
- The midpoint is the center of the curves, located halfway between point F1 and F2. If the parabola is centered at the origin, then the origin is the midpoint.
- The asympototes show where the curve is headed. Although these are not technically part of the shape, they can be helpful with sketching the shape.
- The axis of symmetry splits the two branches exactly down the middle.
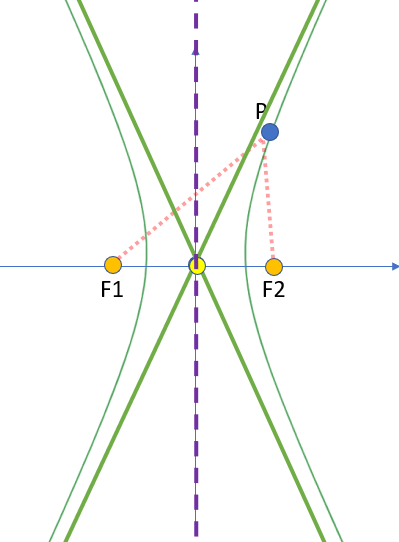
If the hyperbola is centered at the origin with its foci on the x-axis (as in the above image), the equation is:
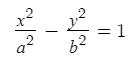
If the foci are on the y-axis, the equation is:
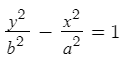
The equation can also be formatted as a second degree equation with two variables [1]:
Ax2 – Cy2 + Dx + Ey + F = 0 or
-Ax2 – Cy2 + Dx + Ey + F = 0.
Hyperbola and Conic Sections
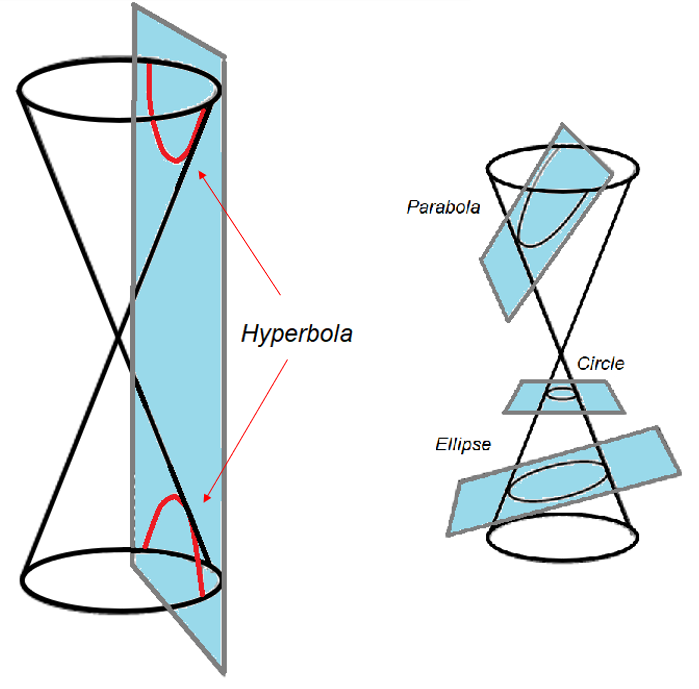
The hyperbola, along with the ellipse and parabola, make up the conic sections. You can get a hyperbola by slicing through a double cone. The difference between this shape and a run-of-the-mill parabola is that the slice is steeper. The slice doesn’t have to be parallel to the cone’s axis, but it does have to create symmetrical curves [2].
References
[1] Bonds, D. Math 155, Lecture Notes-Bonds. Section 10.1 Conics and Calculus.
[2] Hyperbola. Retrieved July 30, 2021 from: http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Kim/emat6690/instructional%20unit/hyperbola/Hyperbola/Hyperbola.htm