Pairwise Independent, Mutually Independent: Definition, Example

Probability > Mutually Independent and Pairwise Independent

Contents:

What is Pairwise?
Averages (Walsh Averages)
Comparison
Differences
Independent / Mutually Independent.
Statistics
Slopes

What is Pairwise?

Pairwise means to form all possible pairs — two items at a time — from a set. For example, in the set {1,2,3} all possible pairs are (1,2),(2,3),(1,3).

Pairwise Averages (Walsh Averages)

Pairwise (Walsh) averages are averages calculated from each pair in a set, including a pair matched with itself. For example, the set {2,9} has three pairs: (2,2),(9,9) and (2,9). The Walsh averages for this set are:

(2,2) = 2
(9,9) = 9
(2,9) = 5.5.

Following this, Walsh averages are used in tests like the Signed-Rank Wilcoxon and other nonparametric tests. In the Wilcoxon signed rank tests, the test statistic is equal to the number of positive Walsh averages (called “offsets”). The formal formula is: (D₁ – D₂)/2, where D is a data point.

Pairwise Comparison

Pairwise comparison is the act of forming pairs with the goal of comparing them in some way. It’s used for head to head comparisons. Each candidate is pitted against every other candidate with points awarded for a “win”. The person/item with the most wins is declared the winner.

Example: Let’s say Washington, Garfield, LBJ and Kennedy ran for election today. The results are tallied for the first 4 states reporting:

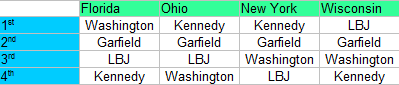
In order to find out who is in the lead, we need to know who won most of the match ups. There are several ways you can do this. Perhaps the easiest is a two way table. I’ve blocked out duplicate squares (e.g. Washington/Garfield is in one square while Garfield/Washington is in another) and any square where a person is pitted against themselves (e.g. Washington/Washington):

Next, fill in the winners of each head to head. I’m assigning 4 points for 1st place, 3 points for 2nd place, 2 points for 3rd place and 1 point for fourth place.

Washington: 4 + 1 + 2 + 2 = 9 points.
Garfield: 3 + 3 + 3 + 3 = 12 points.
LBJ: 2 + 2 + 1 + 4 = 9 points.
Kennedy: 1 + 4 + 4 + 1 = 10 points.

Each pair is matched head to head. For example, Garfield (with 12 points) wins over Washington (9 points) and Garfield/LBJ is a tie:

Just by looking at the results we can see that Garfield has the most “wins.”

If the answer isn’t obvious, award 1 point for a win and 1/2 point for a tie. The results for this match up would be:

Washington: 1/2 point
Garfield: 3 points
LBJ: 1.2 point
Kennedy: 2 points

Pairwise Differences

To find pairwise differences for two equal length columns:

Pair each value in one column with each value in a second column.
Calculate the differences.

Example:

Pair each value in column A with each value in column B: (3,7), (3,2), (3,10), (4,7), (4,2), (4,10), (5,7), (5,2), (5,10).
Calculate the differences between each pair. For example, the difference for the first pair is 3 – 7 = -4, the second pair is 3 – 2 = 1 and the third pair is 3 – 10 = -7. In all, you’ll have a total of 9 differences for this set.

Pairwise Slopes

Pairwise slopes are also calculated for columns of data, except each column represents X and Y values. The slopes are calculated for each pair. For example, let’s say you had the following two columns of data:

A scatter plot of the data would look like this:

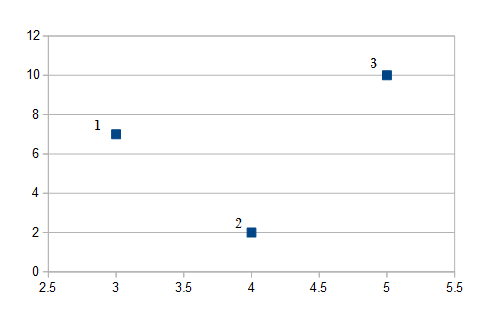
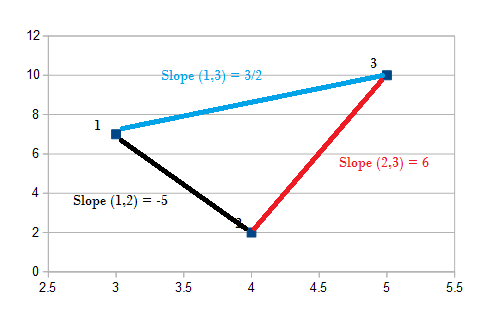
To start, jfust use the slope formula (from elementary algebra) to find the slopes for each pair. For this example there are three pairs (1,2), (1,3), (2,3), so using the slope formula (y₂ – y₁) / (x₂ – x₁):
1st. Slope (1,2) = (2-7)/(4-3) = -5/1 = -5
2nd. Slope (1,3) = (10-7)/(5-3) = 3/2
3rd. Slope (2,3) = (10-4)/(5-4) = 6/1 = 6

Pairwise Independent / Mutually Independent

What is “Pairwise Independent”?

Pairwise Independent means that each event is independent of of every other possible combination of paired events. In other words, the probability of one event in each possible pair (e.g. AB AC BC) has no bearing on the probability of the other event in the pair.

What is Mutually Independent?

Events A, B, and C are mutually independent if they are pairwise independent:
P(A ∩ B) = P(A) × P(B) and…
P(A ∩ C) = P(A) × P(C) and…
P(B ∩ C) = P(B) × P(C)
And:
P(A ∩ B ∩ C) = P(A) × P(B) × P(C), which is stating that their probabilities, when multiplied together, is also the probability of the intersection of the three events.

By definition, mutually independent events are also pairwise independent. But a set of events that is pairwise independent isn’t automatically mutually independent. They must also meet the condition P(A ∩ B ∩ C) = P(A) × P(B) × P(C).

Example Problem

Question: You toss a fair coin twice. The possible events are:

Both tosses give the same outcome (HH or TT).
The first toss is a heads (HT HH).
The second toss is heads (TH HH).

Are the events mutually independent?

Answer:
What the question is really asking is: do these events fit the definition stated above (right under What is Mutually Independent?. The definition states that the following must be true:
P(A ∩ B ∩ C) = P(A) × P(B) × P(C),
So we need to figure out a few probabilities first from the given information.

P(event 1), P(event 2), and P(3).
You have four possible outcomes (HH, TT, TH, HT) so the probability of each pair happening is 0.25. This would make the probabilities of the events 1,2, and 3:

Both tosses give the same outcome (HH or TT) = 1/4 + 1/4 = 1/2.
The first toss is a heads (HT HH) = 1/4 + 1/4 = 1/2..
The second toss is heads (TH HH) = 1/4 + 1/4 = 1/2..

Multiply the probability of events together:
P(1) * P(2) * P(3) = 1/2 * 1/2 * 1/2 = 1/8.

P(1 ∩ 2) = P(1 ∩ 3) = P(2 ∩ 3) = 1/4.
This is because HH is the only event that intersects (a 1 out of 4 probability). If you have trouble figuring out intersections, a Venn diagram is always a good idea. the following diagram should help you see that HH is the intersection for all three probabilities:

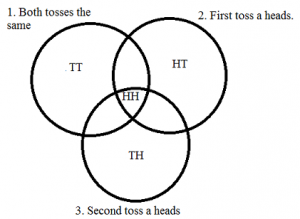
This also gives us P(1 ∩ 2 ∩ 3 ∩) = 1/4.

Now you can compare the two:
P(1 ∩ 2 ∩ 3) = P(1) × P(2) × P(3)
1/8 ≠ 1/4
These are not equal, so the events are not mutually independent.

Pairwise statistics

These are statistics calculated from pairs of observations. In other words, you form pairs of observations and then find a statistic of interest, like a mean or standard deviation.

References:
Rosenbaum, P. Exact Confidence Intervals for Nonconstant Effects by Inverting the Signed Rank Test. The American Statistician, May 2003, Vol. 57, No. 2 Retrieved October 8, 2016 from here. url: http://stat.wharton.upenn.edu/~rosenbap/offsetEdit.pdf