Bow Curve

Quartic curves >

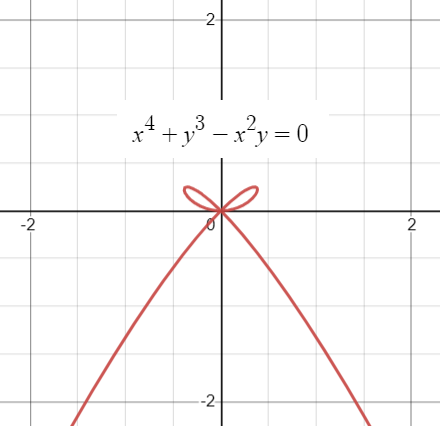
A bow curve is a quartic (4th degree) curve defined by the Cartesian equation [1]:
x⁴ + y³ – x²y = 0.

It is also defined by the parametric equation
x = t – t³, y = t² – t⁴.
and the polar equation

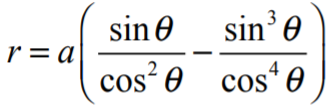
Other Bow-Shaped Curves

The curve defined above is sometimes called the quartic bow curve, presumably to distinguish it from other, similar curves shaped like bows.

Some authors use the name “bow curve” without clarifying which type of bow-shape they are referring to, which can get confusing. For example, Guo [2] mentions a shape constructed with a “bow curve” on page 174. However, the image the paragraph refers to (figure 3.3. on page 175) is clearly a longbow curve, parameterized by the equations [3]
x(θ) = a (sin²θ + 1) cost(θ); y(θ) = a (sin²θ + 1).

Make sure you know which type of “bow” curve you’re being asked to analyze or draw.

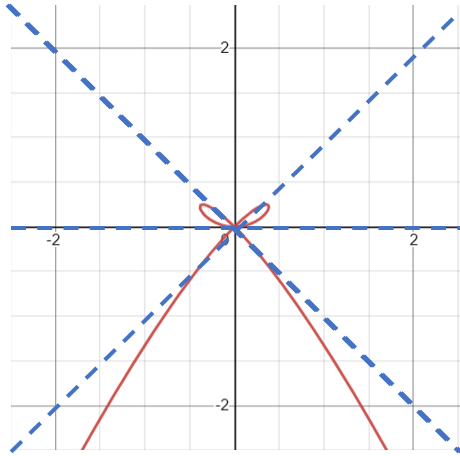
Tangent Lines of the Bow Curve

The bow curve has three tangent lines (i.e., a triple point) at the origin. A triple point is a point on a curve where three branches of the curve intersect; in other words, it’s a point traced three times when the curve is traversed.

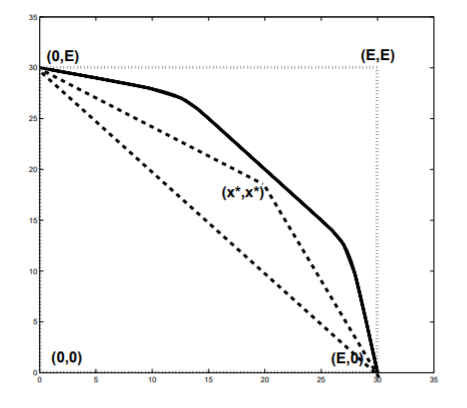
The Spectahedron

The curve can fit inside a third order spectrahedron—a shape that can be represented as a linear matrix inequality. In two dimensions, the spectrahedron looks like a trapezoid:

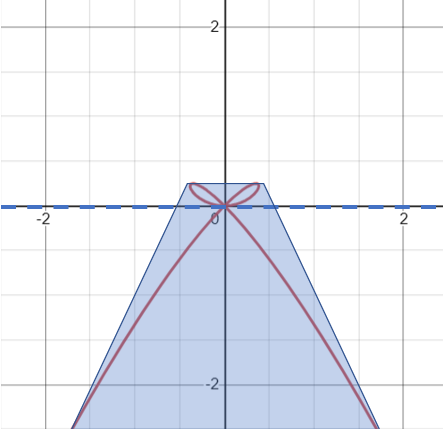
Uses

This curve has limited, if an, practical uses. Its main use is purely academic, appearing in some texts as either to study interesting curve behavior or triple points.

References

Graphs created with Desmos.
[1] Ingalls, C. Bow Curve. Retrieved January 1, 2022 from: https://people.math.carleton.ca/~cingalls/studentProjects/Katie’s%20Site/html/Bow%20Curve.html
[2] Guo, F. et al. Semidefinite Representation of Non-Compact Convex Sets.
[3] M243: Calculus II (Sp 2019).