Contents:
- What is a Critical Number?
- Critical Point vs. Critical Value
- How to find critical numbers
- Stationary Points
What is a Critical Number?
A critical number (or critical value) is a number “c” that is in the domain of the function and
either:
- Makes the derivative equal to zero: f′(c) = 0, or
- Results in an undefined derivative (i.e. it’s not differentiable at that place): f′(c) = undefined.
Critical numbers indicate where a change is taking place on a graph. For example:
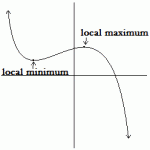
- An increasing to decreasing point (e.g. a local maximum), or
- A decreasing to increasing point (e.g. a local minimum).
The number “c” has to be in the domain of the original function (the one you took the derivative of). If the number isn’t in the domain (for example, if there is a removable discontinuity at x = 0), then that number isn’t a critical number. It’s for this reason (there might be a miniscule hole in the graph), that you can’t rely on a graph to find critical numbers. In general, you have to find them with algebra.
Watch the video for the definition and two examples:
Critical Point vs. Critical Value
The terms critical value (or number) and critical point are sometimes used interchangeably. However, there is a subtle difference between the two. Critical values are all maxima, minima, or points of inflection. On the other hand, critical points are sometimes defined as a point in the function’s domain where the function is not differentiable or equal to zero. Like many terms in math, there isn’t a hard and fast rule about this or a formal definition that’s standard across the board. Therefore, you’ll want to refer to your teacher (or textbook) to make sure of the exact definition.
How to find critical numbers
Finding critical numbers is relatively easy if your algebra skills are strong; Unfortunately, if you have weak algebra skills you might have trouble finding critical numbers. Why? Because each function is different, and algebra skills will help you to spot undefined domain possibilities like division by zero. If your algebra isn’t up to par—now is the time to restudy the old rules.
Example question 2: Find the critical numbers for the following function:
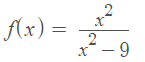
Step 1: Take the derivative of the function. Which rule you use depends upon your function type. For this example, you have a division, so use the quotient rule to get:
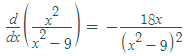
Step 2: Figure out where the derivative equals zero. This is where a little algebra knowledge comes in handy, as each function is going to be different.
For this particular function, the derivative equals zero when -18x = 0 (making the numerator zero), so one critical number for x is 0 (because -18(0) = 0).
Another set of critical numbers can be found by setting the denominator equal to zero; When you do that, you’ll find out where the derivative is undefined:
- (x2 – 9) = 0
- (x – 3)(x + 3) = 0
- x = ±3
Step 3: Plug any critical numbers you found in Step 2 into your original function to check that they are in the domain of the original function. For this function, the critical numbers were 0, -3 and 3. Let’s plug in 0 first and see what happens:
f(x) = 02⁄02-9 = 0. Therefore, 0 is a critical number.
For +3 or -3, if you try to put these into the denominator of the original function, you’ll get division by zero, which is undefined.
f(x) = 32⁄32-9 = 9/0. Therefore, 3 is not a critical number.
That means these numbers are not in the domain of the original function and are not critical numbers.
That’s it!
Back to Top.
Stationary Points
A stationary point is the point at which the derivative is zero; where
f′(x0) = 0.
Stationary points include minimums, maximums, and inflection points; but not all inflection points are stationary points.
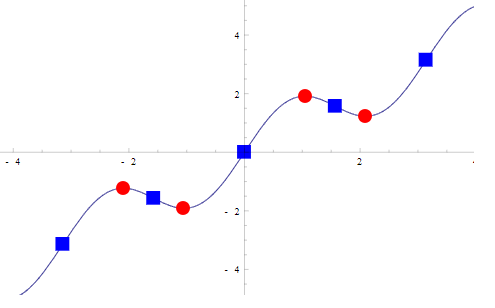
Stationary points are called that because they are the point at which the function is, for a brief moment, stationary: neither decreasing or increasing.
Using Stationary Points for Curve Sketching
Stationary points can help you to graph curves that would otherwise be difficult to solve. They include most of the interesting points on the curve, and if you graph them, and connect the dots, you have a fairly good general curve of your function.
You will want to know, before you begin a graph, whether each point is a maximum, a minimum, or simply an inflection point. One way to do this is by looking at the second derivative.
If the second derivative is less than 0, the stationary point is a maximal extremum, and the graph is concave down right at that point.
- If the second derivative is greater than zero, the stationary point is a minimal extremum, and the graph is concave up at that point.
- If the second derivative is equal to zero, you’ll have to use other methods to determine what kind of stationary point it is. You might look at the sign change around that point, for example.
References
Difeng, C. MATH 111 Calculus I : 4.1 Maximum and Minimum Values. Retrieved August 18, 2021 from: http://www.math.emory.edu/~dcai7/day15.html
Patrikalakis, Maekawa, & Cho. Classification of stationary points. 7.3.1 in Shape Interrogation for Computer Aided Design and Manufacturing (Hyperbook Edition) Retrieved from http://web.mit.edu/hyperbook/Patrikalakis-Maekawa-Cho/node138.html on Feb 19, 2019
University of East Anglia Learning Enhancement Team. Steps Into Calculus: Finding Stationary Points. Retrieved from https://portal.uea.ac.uk/documents/6207125/8199663/steps+into+calculus+finding+stationary+points.pdf on Feb 20, 2019.