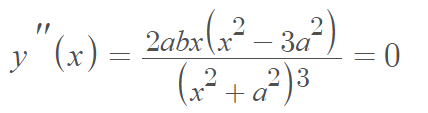The serpentine curve, named because of its snakelike shape, is a cubic curve defined by the Cartesian equation [1]
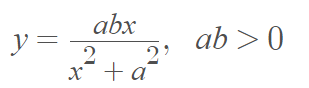
or by the parametric equations
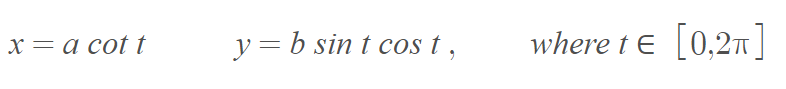
The serpentine is a subcase of one of the normal forms of the cubic curve f(x, y) = 0:
xy2 + ey = ax3 + bx2 + cx + d [1].
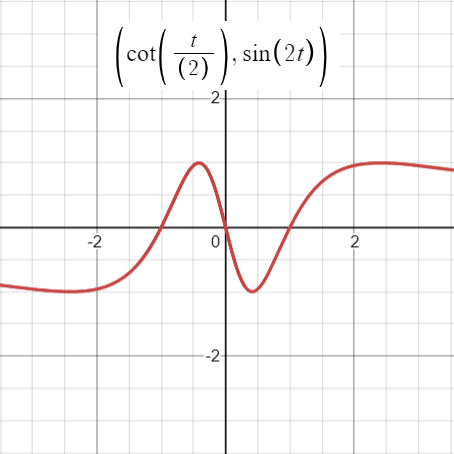
Serpentine Curve Properties
- Local maximum at x = a and Local minimum at x = -1,
- Inflection points are at x = ± √(3a), where the second derivative equals zero, i.e.,[2]

Where the first derivative is zero, i.e.,:
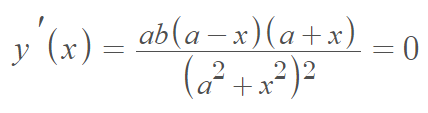
History
The serpentine curve was first studied by L’Hôpital and Huygens in 1692. Later, it was studied by Newton, in 1701, who gave the curve its name [3]. It appears in the 1710 work Curves by Sir Isaac Newton in Lexicon Technicumby John Harris [1].
Applications of the Serpentine Curve
Snakes, perhaps not surprisingly, move in the pattern of a serpentine curve. According the Hirose [4], that’s because the curve has the “greatest amount of smoothness of contraction and relaxation of the motor muscles”. The model for snake movement is a little more challenging than the generic serpentine curve proposed by Newton:
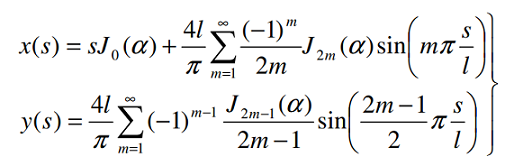
Where:
- α is the winding angle,
- jm is the mth order Bessel function.
Serpentine curves are also used in surveying, where they are also called S-curves. They are generally used to connect two railway lines or parallel roads intersect at a tiny angle [5].
In engineering, the trajectory of a Chaplygin sleigh with periodic actuation is a serpentine curve [6].
References
[1] Mactutor. Serpentine. Retrieved March 6, 2022 from: https://mathshistory.st-andrews.ac.uk/Curves/Serpentine/
[2] Weisstein, Eric W. “Serpentine Curve.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/SerpentineCurve.html
[3] Titu Maiorescu University. The International Conference Education and Creativity for a Knowledge based Society – Computer Science, 2012.
[4] S. Hirose. Biologically Inspired Robots: Snake-Like Locomotors and
Manipulators. Oxford University Press, 1993. Cited in Spranklin, B. DESIGN, ANALYSIS, AND FABRICATION OF A SNAKE-INSPIRED ROBOT WITH A RECTILINEAR GAIT. 2006.
[5] Types of Curves in Surveying. Retrieved March 6, 2022 from: https://dailycivil.com/types-of-curves-in-surveying/
[6] Fedonyuk, V. (2020). Dynamics and Control of Nonholonomic Systems with Internal Degrees of Freedom. Retrieved March 6, 2022 from: https://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=3650&context=all_dissertations