The Klein quartic, named after Felix Klein, is an algebraic curve with equation x3y + y3z + z3x = 0 [1]. It can be defined by a fourth degree equation in complex homogeneous coordinates, hence the name the Klein quartic curve [2].
Symmetry of The Klein Quartic
The Klein quartic is famous for its abundance of symmetry: The curve gives the
compact Riemann surface of genus 3 with 168 automorphisms. This is the maximum number possible for a curve of this type by the Hurwitz bound. In more simple terms, it has 168 symmetries, but if you include mirror reflections it has 336. It has 24 heptagons, and a symmetry sends any of these heptagons to any other of those 24. It can also be rotated 7 ways, for a total of 168 symmetries (twice that number if you allow reflections) [3].
The Klein quartic can be thought of as an extension of Platonic solids to a hyperbolic heptagonal tiling [4]. As such, it can’t be rendered exactly in three-dimensions, but the following animation is “close enough” to get an idea of the geometry. If you look closely at the following animation you can see that each colored “wedge” is a triangle; seven triangles meet at each vertex. Topologically speaking, the Klein quartic is a three-holed torus [5], which gives it trilateral symmetry.
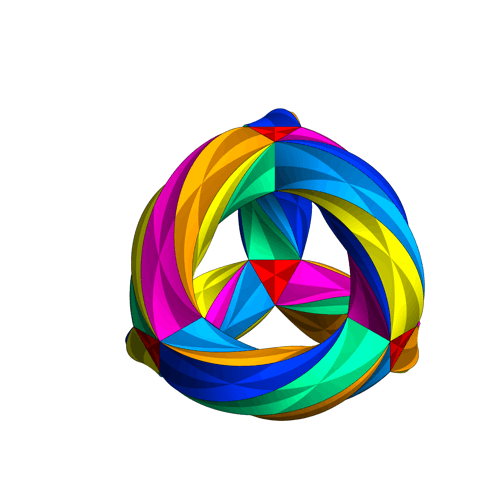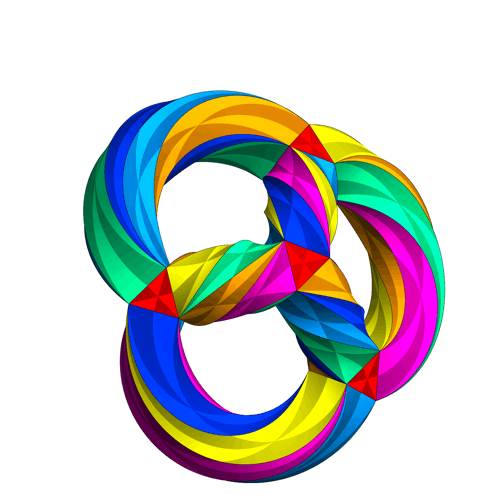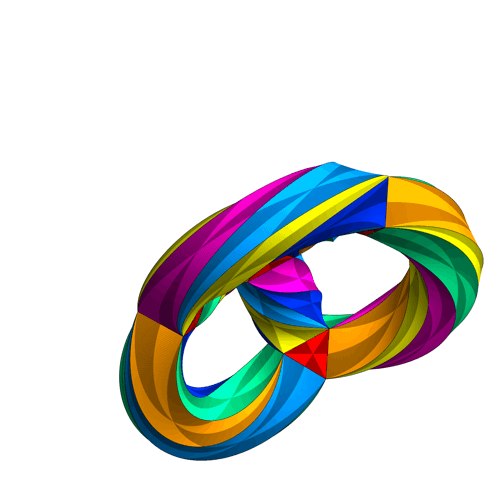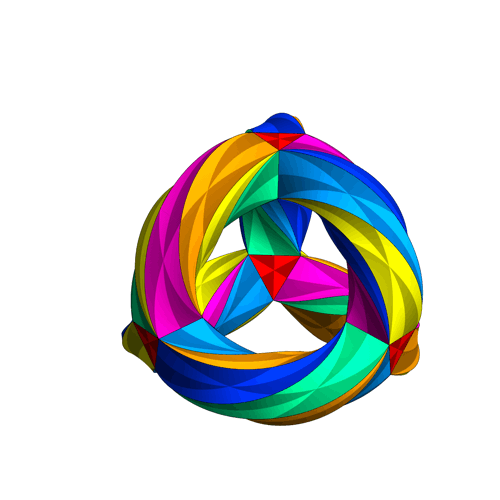
The Klein quartic was introduced by Klein in volume 14 of Mathematische Annalen (1878/79) [6]. An updated version appeared in Klein’s Collected Works [7], which is in German. The Eightfold Way the beauty of Klein’s Quartic curve [8] contains an English translation.
Notes:
A Riemann surface: A surface that covers the complex
plane with “sheets” that can have complicated structures and interconnections. In simpler terms, it is a surface that represents the domain of complex functions [9].
An Automorphisms is an isomorphism from one group to itself. In a very basic way, it can considered as the symmetry of the Klein quartic surface [9].
References
Klein’s Quartic image. Greg Egan,
[1] Ivrissimtzis, I. et al. FROM FAREY FRACTIONS TO THE KLEIN QUARTIC AND BEYOND. Retrieved January 13, 2022 from: http://arxiv-export-lb.library.cornell.edu/pdf/1909.08568
[2] Vogeler, R. (2003). On the Geometry of Hurwitz Surfaces.
[3] Baez, J. (2013). Klein’s Quartic Curve. Retrieved January 13, 2022 from: https://math.ucr.edu/home/baez/klein.html
[4] Coxeter, H. S. M. “Regular Honeycombs in Hyperbolic Space.” In Proceedings of the International Congress of Mathematicians, 1954, Amsterdam, Vol. 3. Groningen, Netherlands: Noordhoff, pp. 155-169, 1956. Reprinted as Ch. 10 in The Beauty of Geometry: Twelve Essays. New York: Dover, pp. 200-214, 1999.
[5] Baez, J. (2005). This Week’s Finds in Mathematical Physics (Week 215).
[6] Felix Klein. Ueber die transformation siebenter ordnung der elliptischen functionen. Mathematische Annalen, 14(3):428–471, 1878.
[7] Felix Klein. Gesammelte Mathematische Abhandlungen: Dritter Band: Elliptische Funktionen, Insbesondere Modulfunktionen Hyperelliptische und
Abelsche Funktionen Riemannsche Funktionentheorie und Automorphe Funktionen. Springer Berlin Heidelberg, 1923.
[8] Silvio Levy. The eightfold way: the beauty of Klein’s quartic curve, volume 35.
Cambridge university Press, 2001.
[9] Bhattaram, A. (2020). Klein’s Quartic. Retrieved January 13, 2022 from: http://simonrs.com/eulercircle/rtag2020/amulya-klein.pdf