When to Find the Area Between Curve and Y-Axis
You’ll need to integrate with respect to y when working with double integrals and triple integrals. You’ll sometimes need to use the method when working with solids of revolution, when you can integrate with respect to x or y.
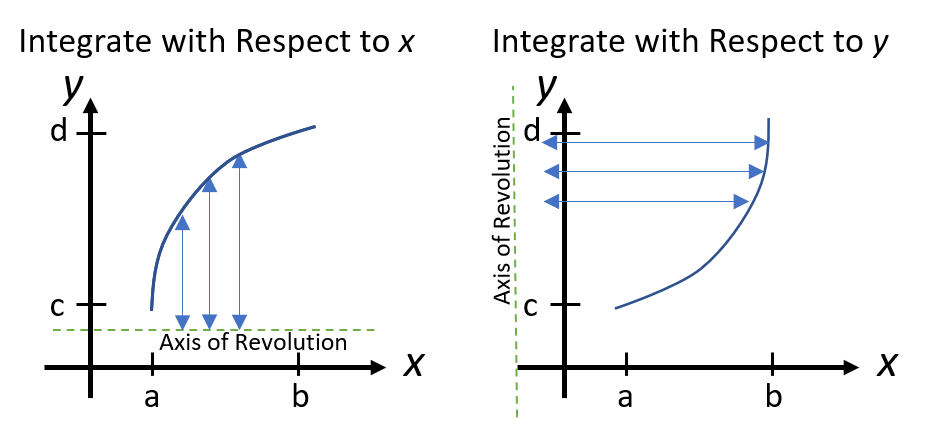
Which method you choose for evaluating solids of revolution depends on what your shape looks like (which is why it’s always a good idea to start by sketching your shape, if you can visualize it). But often it’s a matting or guessing whether you should integrate with respect to y (using horizontal slices), or with respect to x (using vertical slices); Both types of integration will result in the same volume, so pick whichever works best.
There are a couple of disadvantages to working with horizontal slices (i.e. differentiating with respect to y):
- The “usual” way of integration is something like muscle memory. If you’re used to performing integration with respect to x, you may find it challenging to re-adjust to working with a different method (like treating “x” expressions like x2 as constants).
- You have to invert the function(s) you’re dealing with. For example, if your function is y = f(x) you’ll have to express x as a function of y instead [1].
Example of Area Between Curve and Y-Axis (Double Integrals)
The following double integral (representing volume) requires you to work the “inside” integral first, with respect to y:
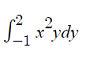
→
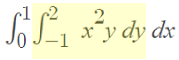
Step 1: Take out the constant. We’re treating our entire x-expression as a constant here:
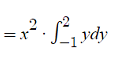
Step 2: Apply the power rule:
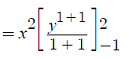
Step 3: Simplify:
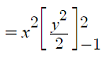
Step 4: Calculate the boundaries:
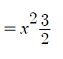
Step 5: Insert your solution back into the original question then integrate with respect to x:
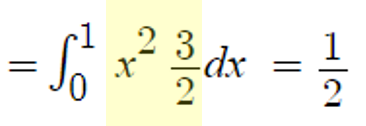
For more examples, See:
References
[1]Harbourne, B. How in general to set up your integral for computing volume. Retrieved May 7, 2021 from: https://www.math.unl.edu/~bharbourne1/M107Spr04/volreview/vol.html