Quartic Curves > Cruciform Curve
The cruciform curve, also called the cross curve, policeman on point duty curve [1], or stauroid [2], is a plane curve defined by the implicit equation x2y2 – a2x2 – b2y2 = 0.
Additional equations [3]:
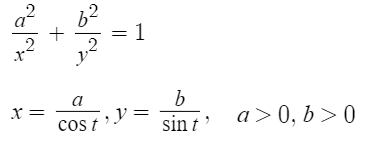
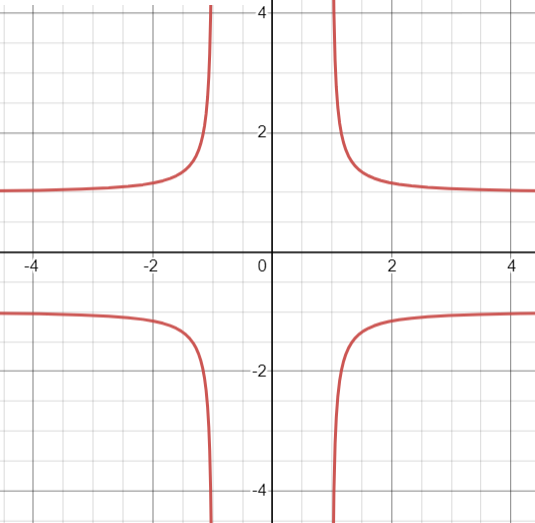
You can see the above graph on Desmos, which has sliders for different values of a and b. A special case is the circular cruciform curve (a = b) [2].
Etymology and History
The word cruciform is from the Latin crux, stem cruc– (a cross) and forma (form, figure, shape) [4]. The first known study of the cruciform curve was in 1847, in relation to a question by the French mathematician Olry Terquem [5].
Properties of the Cruciform Curve
Thirteen years after Terquem studied the curve, the Italian mathematician Francesco Siacci demonstrated an interesting property of the cross curve: “…the sum of the areas limited by the four branches of the curve and by the respective asymptotes is equal to the area of the rectangle formed by the same asymptotes.” [6]
- The cruciform curve is an algebraic curve of degree 4.
- It has four unbounded branches.
- It also has four asymptotes at straight lines x±a = 0 (two vertical asymptotes) and y±b = 0 (two horizontal asymptotes).
- The curve has two lines of symmetry at x = 0 and y = 0 with central symmetry at (0, 0).
Practical Uses for the Cruciform Curve
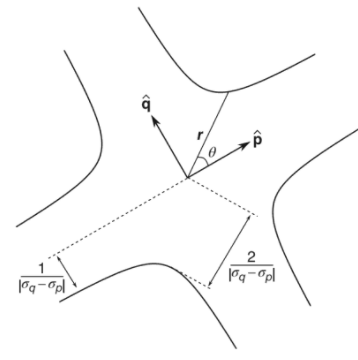
The cruciform curve can be seen in the shear stress quartic, which is a way to visualize shear stress components of solid surfaces in mechanical engineering [7]:
References
[1] Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 71, 1989.
[2] Wassenaar, J. 2dCurves. PDF Retrieved February 10, 2022 from: https://rs.1lib.to/book/499576/3dfc18
[3] Shikin, E. Handbook and Atlas of Curves. CRC Press. 2014.
[4] Schwartzman, S. The Words of Mathematics. An Etymological Dictionary of Mathematical Terms Used in English. Mathematical Association of America. 1994.
[5] Terquem, O. Question 165, Nouvelles Annales des mathematiques, 1re serie, Paris: tome 6, 394. 1847.
[6] Ritelli, D. & Scimone, A. Some hidden harmonies between new and old geometric loci. Elemente der Mathematik 69(4):178-185. 2014.
[7] Jenkins, S. Chirality at Solid Surfaces. Wiley. 2018.