A Lamé curve (also called a Lamé Oval) has the Cartesian equation
Where n is a positive real number.
The Lamé curve is sometimes called a superellipse, but the superellipse is actually a particular case when n > 2 [1].
Lamé curves were named after mathematician Gabriel Lamé (1795-1870), but it was Julius Plucker (1801-1866) who advanced their study [1].
Properties of a Lamé curve
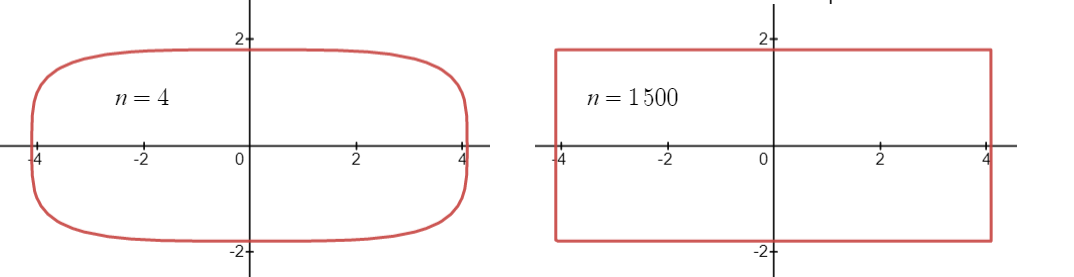
The b controls the y-axis; the a variable controls the x-axis. When a = b, the two axes are equal and the curve is a supercircle or a subcircle.
The variable n has many interesting properties [2]:
- When n is rational, the curve is algebraic.
- When n is irrational, the curve is transcendental.
- If n is an even integer, the curve looks more like a rectangle as n increases.
- When n = 0, the curve reduces to a pair of crosses lne.
- If n is a positive integer, the curve is closed [3].
- When n = 1, the curve is a straight line [4].
- When n = 2, the equation becomes the standard form for an ellipse. The ellipse is the only Lamé curve to have foci and the concept of eccentricity [5].
- When n = ⅔ the curve is an Astroid.
- when n > 2, the curves are called superellipses.
1970s Danish artist and designer Piet Hein is often credited with bring the Lamé Curve out of obscurity. The designer used superellipses, with his preferred choice of 4:3 for variables a and b, to design a variety of ellipse-like tabletops, windows, and architectural designs, including a sunken plaza in the city of Stockholm [5].
References
Graphs created with Desmos.com.
[1] MacTutor. Lamé Curves. Retrieved February 22, 2022 from: http://www-groups.dcs.st-and.ac.uk/~history/Curves/Lame.html
[2] Hembree, D. Super Ellipse and His Sidekick Astroid.
[3] Resnikoff, H. & Wells, R. (2015). Mathematics in Civilization, Third Edition. Dover Publications.
[4] Hazelwinkel, M. (2013). Encyclopaedia of Mathematics. Springer Netherlands.
[5] Gridgeman, N. Lamé Ovals. The Mathematical Gazette Vol. 54, No. 387 (Feb., 1970), pp. 31-37. The Mathematical Association