Contents (Click to skip to that section):
- What is a Transformation?
- Common Transformation Types (for data)
- How to Graph Transformations
- Other Transformations in Matrices, Regression & Hypothesis Testing
See also: Affine Transformation
What is a Transformation?
In layman’s terms, you can think of a transformation as just moving an object or set of points from one location to another. You literally “transform” your data into something slightly different. For example, you can transform the sequence {4, 5, 6} by subtracting 1 from each term, so the set becomes {3, 4, 5}.
The many reasons why you might want to transform your data include: reducing skew, normalizing your data or simply making the data easier to understand. For example, the familiar Richter scale is actually a logarithmic transformation: an earthquake of magnitude 4 or 6 is easier to understand than a magnitude of 10,000 or 1,000,000.
More formally, transformations over a domain D are functions that map a set of elements of D (call them X) to another set of elements of D (call them Y). The relationships between the elements of the initial set are typically preserved by the transformation, but not necessarily preserved unchanged.
The image below shows a piece of coding that, with four transformations (mappings) converts a simple rectangular repeated pattern into a rhombic pattern.

Transformation Types
The word transformation is used most often in geometry. Types of transformations in geometry include translations (shifts, scales, and reflections) rotation, and shear mapping. But more generally, a transformation can mean any kind of mathematical function.
In general, you can transform a function in seven basic ways. For a function y = f(x):
- y = f(x – c): Horizontal shift c units right
- y = f(x + c): Horizontal shift c units left
- y = f(x) – c: Vertical shift c units down
- y = f(x) + c: Vertical shift c units up
- y = -f(x): Reflection over the x-axis
- y = f(-x): Reflection over the y-axis
- y = -f(-x): Reflection about the origin.
Specific ways to transform include:
- Taking the logarithm. Log Transformation is where you take the natural logarithm of variables in a data set.
- Square root transformations. Simply take the square root of your variables, i.e. x → x(1/2) = sqrt(x). This will have a moderate effect on the distribution and usually works for data with non-constant variance. However, it is considered to be weaker than logarithmic or cube root transforms.
- Taking the square: x → x2 can reduce left skewness. It has a medium effect on data.
- Reciprocal Transformations: the reciprocal transformation x → 1/x has a very large change on the shape of a distribution and reverses the order of values with the same sign; The negative reciprocal, x to -1/x, also has a drastic effect but preserves the variable order. This can be a particularly useful transformation for a set of positive variables where a reverse makes sense. For example, if you have number of patients per doctor, you can transform to doctors per patient (Cox, 2005).
- Box Muller Transform (Statistics): transforms data with a uniform distribution into a normal distribution.
- Differencing (Statistics): differenced data has one less point than the original data. For example, given a series Zt you can create a new series Yi = Zi – Zi – 1.
- Fitting a curve to the data: In modeling, after you have fit a curve, you can then model the residuals from that curve. Curve fitting algorithms include: gradient descent, Gauss-Newton and the Levenberg–Marquardt algorithm.
- Cube Root Transformations: x → x(1/3) is useful for reducing right skewness. Can be applied to positive and negative values.
Transformations in Geometry
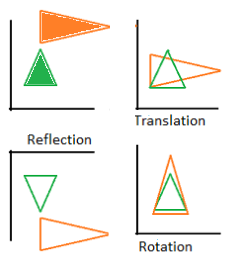
- Shift: moves every point by the same distance in the same direction.
- Reflection: a folding or flipping over a certain line (e.g.the y-axis).
- Glide reflections: a combination of a reflection and a shift.
- Rotation: turns a figure about a fixed point (a center of rotation).
- Scaling: Enlarges, or shrinks, an object by the same scale factor.
- Shear mapping: all points along one line stay fixed, while other points are shifted parallel to the line by a distance proportional to their perpendicular distance from the line.
Using Transformations to Graph Functions
Sometimes we can use the concept of transformations to graph complicated functions when we know how to graph the simpler ones.
For example, if you know the graph of f(x), the graph of f(x) + c will be the same function, just shifted up by c units. f(x) – c will be the same thing, too, just shifted down by c units. The graph of f(x + c) s the graph of f(x), shifted left by c units, and the graph of f(x – c) is the graph of f(x) shifted right by c units. For a few step by step examples of vertical (up/down) shifts, see: Vertical Shift of a Function
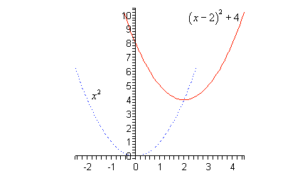
As an example, take the graph of f(x) = (x-2)2 + 4. We might not know what that looks like, but we do know what h(x) = x2 looks like—a simple upward facing parabola. Imagine sketching that, then shift it to the right by 2 and up by 4. Then you have the sketch of f(x).
Vector Transformation
A vector transformation is a specific type of mapping where you associate vectors from one vector space with vectors in another space.
What is a vector space?
The concept of a vector space is fundamental to understanding vector transformations. A vector space is a collection of vectors which can be added and multiplied by scalars. Vectors have both magnitude and direction (e.g. 10 mph East).
A vector space has two requirements. Without leaving the vector space,
- Any two vectors can be added.
- Any two vectors can be scaled (multiplied).
Vector Spaces are often defined as Rn vector spaces, which are spaces of dimension n where adding or scaling any vector is possible. R stands for “Real” and these spaces include every vector of the same dimension as the space. For example, the R2 vector spaces includes all possible 2-D vectors. For example, the vectors (4, 2), (19, 0), and (121, 25) are all 2-D vectors (ones that can be represented on an x-y axis). The vector space R3 represents three dimensions, R,4 represents four dimensions and so on.
It’s practically impossible to deal with Rn vector spaces, because they contain every possible vector of n dimensions, up to infinity. Instead, we use subspaces, which are smaller vector spaces within a Rn vector space.
Back to Top
The Role of Functions in Vector Transformations
Vector transformations can be thought of as a type of function. For example, if you map the members of a vector space Rn to unique members of another vector space Rp, that’s a function. It’s written in function notation as:
f: Rn → Rp
Vector Transformation Example
Let’s say you had a vector transformation that mapped vectors in an R3 vector space to vectors in an R2 space. The general way to write the notation is:
f: R3 → R2
A specific example:
f(x1, x2, x3) = (x1 + 3x2, 4x3)
Note that f(x1,x2,x3) has three vectors and so belongs in ℝ3 and (x1 + 3x, 4x3) has two vectors and so belongs in ℝ2.
This example could also be written as:
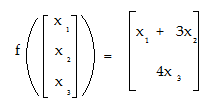
Working out the vector transformation is equivalent to working out a function and involves some basic math. For example, let’s say you had the function f: x→ x2 and you wanted to transform (map) the number 2. You would insert it into the right hand part of the equation to get 22 = 4. Vector transformation works the same way.
For example, performing a vector transformation from f(2, 3, 4) to (X1 + 3x2, 4x3) we get:
- X1 = 2
- X2 = 3
- X3 = 4,
so:
(2 + 3(3), 4(4)) = (2 + 9, 16) = (11, 16)
Back to Top
Linear Transformation
Linear transformation is a special case of a vector transformation.
Definition:
Let V And W be two vector spaces. The function T:V→W is a linear transformation if the following two properties are true for all u, v, ε, V and scalars C:
- Addition is preserved by T: T(u + v) = T(u) = T(v). In other words, if you add up two vectors u and v it’s the same as taking the transformation of each vector and then adding them.
- Scalar multiplication is preserved by t: T(cu) = cT(u). In other words, if you multiply a vector u by a scalar C, this is the same as the transformation of u multiplied by scalar c.
How to Figure out if a Transformation is Linear
Applying rules 1 and 2 above will tell you if your transformation is a linear transformation.
Part One, Is Addition Preserved? Works through rule 1 and Part Two, Is Scalar Multiplication Preserved? works through rule 2. Remember: Both rules need to be true for linear transformations.
Example Question: Is the following transformation a linear transformation?
T(x,y)→ (x – y, x + y, 9x)
Part One: Is Addition Preserved?
Step 1: Give the vectors u and v (from rule 1) some components. I’m going to use a and b here, but the choice is arbitrary:
- u = (a1, a2)
- v = (b1, b2)
Step 2: Find an expression for the addition part of the left side of the Rule 1 equation (we’re going to do the transformation in the next step):
(u + v) = (a1, a2) + (b1, b2)
Adding these two vectors together, we get:
((a1 + b1), (a2 + b2))
In matrix form, the addition is:
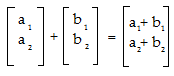
Step 3: Apply the transformation. We’re given the rule T(x,y)→ (x – y, x + y, 9x), so transforming our additive vector from Step 2, we get:
- T ((a1 + b1), (a2+ b2)) =
- ((a1 + b1) – (a2 + b2),
- (a1 + b1) + (a2 + b2),
- 9(a1 + b1)).
Simplifying/Distributing using algebra:
(a1 + b1 – a2 – b2,
a1 + b1 + a2 + b2,
9a1 + 9b1).
Set this aside for a moment: we’re going to compare this result to the result from the right hand side of the equation in a later step.
Step 4: Find an expression for the right side of the Rule 1 equation, T(u) + T(v). Using the same a/b variables we used in Steps 1 to 3, we get:
T((a1,a2) + T(b1,b2))
Step 5: Transform the vector u, (a1,a2). We’re given the rule T(x,y)→ (x – y, x + y, 9x), so transforming vector u, we get:
- (a1 – a2,
- a1 + a2,
- 9a1)
Step 6: Transform the vector v. We’re given the rule T(x,y)→ (x – y, x + y,9x), so transforming vector v, (a1,a2), we get:
- (b1 – b2,
- b1 + b2,
- 9b1)
Step 7: Add the two vectors from Steps 5 and 6:
(a1 – a2, a1 + a2, 9a1) + (b1 – b2, b1 + b2, 9b1) =
((a1 – a2 + b1 – b2,
a1 + a2 + b1 – b2,
9a1 + 9b1)
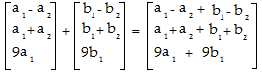
Step 8: Compare Step 3 to Step 7. They are the same, so condition 1 (the additive condition) is satisfied.
Part Two: Is Scalar Multiplication Preserved?
In other words, in this part we want to know if T(cu)=cT(u) is true for T(x,y)→ (x-y,x+y,9x). We’re going to use the same vector from Part 1, which is u = (a1, a2).
Step 1: Work the left side of the equation, T(cu). First, multiply the vector by a scalar, c.
c * (a1, a2) = (c(a1), c(a2))
Step 2: Transform Step 1, using the rule T(x,y)→ (x-y,x+y,9x):
(ca1 – ca2,
ca1 + ca2,
9ca1)
Put this aside for a moment. We’ll be comparing it to the right side in a later step.
Step 3: Transform the vector u using the rule T(x,y)→ (x-y,x+y,9x). We’re working the right side of the rule 2 equation here:
(T(a1, a2)=
a1 – a2
a1 + a2
9a1)
Step 4: Multiply Step 3 by the scalar, c.
(c(a1 – a2)
c(a1 + a2)
c(9a1))
Distributing c using algebra, we get:
(ca1 – ca2,
ca1 + ca2,
9ca1)
Step 5: Compare Steps 2 and 4. they are the same, so the second rule is true. This function is a linear transformation.
Isometry (a Type of Linear Transformation)
An isometry is a linear transformation that preserves distance and length.
The image below shows a linear transformation f that sends A to B and X to Y, while preserving the distance between the points A and B (X and Y) and the length of the line AB (XY). If A and B were 5 cm away originally, the distance between f(A) = X and f(B) = Y, must also be 5 cm.
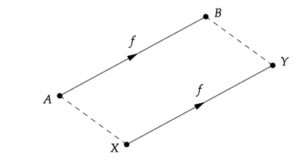
An isometry is also sometimes called a congruence transformation.

Since we call any property that is preserved under a transformation invariant under that transformation, we can say that length and distance are invariant under a congruence transformation. Rotation, shift, reflection, glides, and the identity map are all isometries.
If two figures are related by a congruence transformation (can be transformed into each other by means of an isometry), they are called congruent.
Mathematical Definition of an Isometry
If we have X and Y, two metric spaces with metrics dX and dY, then the map f:X → Y is an isometry if, for every and any a, b in X
dY(f(a)f(b)) = dX(a,b).
Important Properties of Isometries
In the Euclidean plane, any isometry that maps each of three non-collinear points (points that do not all lie on one line) to each other is the identity transformation (the transformation that sends every point to itself).
If an isometry in the plane has more than one fixed point, it is either a reflection (over an axis which crosses that point) or the identity transformation. The image below shows one such reflection; you can see that distances are preserved and the points in the reflection plane—for example, C—remain unchanged under the transformation.
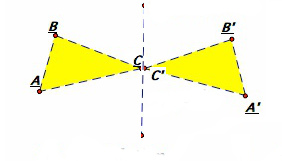
Any isometry on the Euclidean plane can be uniquely determined by two sets of three non-collinear points; points that determine congruent triangles.
Log Transformation of a Skewed Distribution.
Log transformation means taking a data set and taking the natural logarithm of variables. Sometimes your data may not quite fit the model you are looking for, and a log transformation can help to fit a very skewed distribution into a more normal model. As a result, you can more easily see patterns in your data. Log transformation does not “normalize” your data; it’s purpose is to reduce skew.
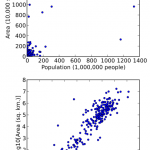
In the image above, it’s practically impossible to see any pattern in the above image. However, in the second image, the data has had a log transformation. Consequently, the pattern becomes apparent.
Log Transformations and Statistical Tests.
If you are running a parametric statistical test on your data (for example, an ANOVA), using data that’s highly skewed to the right or left can lead to misleading test results. Therefore, if you want to perform a test on this kind of data, run a log transformation and then run the test on the transformed numbers.
When Should I Use Log Transformation?
Many possible transformations exist. However, you should only use a log transformation if:
- Your data is highly skewed to the right (i.e. in the positive direction).
- The residual’s standard deviation is proportional to your fitted values
- The data’s relationship is close to an exponential model.
- You think the residuals reflect multiplicative errors that have accumulated during each step of the computation.
Log transformation in Software.
Reciprocal Transformation
The reciprocal transformation is defined as the transformation of x to 1/x. The transformation has a dramatic effect on the shape of the distribution, reversing the order of values with the same sign. The transformation can only be used for non-zero values.
A negative reciprocal transformation is almost identical, except that x maps to -1/x and preserves the order of variables.
How to Graph Transformations
Once you’ve committed graphs of standard functions to memory, your ability to graph transformations is simplified.
The eight basic function types are:
- Sine function,
- Cosine function,
- Rational function,
- Absolute value function,
- Square root function,
- Cube (polynomial) function,
- Square (quadratic) function,
- Linear function.
Each has their own domain, range, and shape. When you transform one of these graphs, you shift it up, down, to the left, or to the right. Being able to visualize a transformation in your head and sketch it on paper is a valuable tool. Why? Sometimes the only way to solve a problem is to visualize the transformation in your head. While graphing calculators can be a valuable tool in developing your mathematical knowledge, eventually the calculator will only be able to help you so much.
Graph Transformations: Steps
Example Problem 1: Sketch the graph of x3 shifted two units to the right and then write the equation for that graph.
Step 1: Visualize the graph of x3, which is a cube (polynomial).
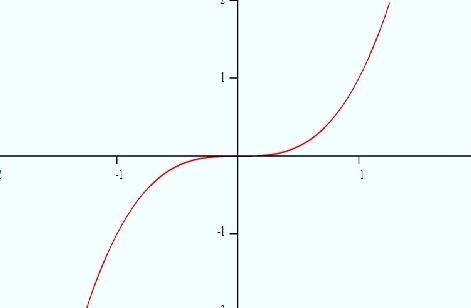
Step 2: Visualize the transformation. All you’re doing is shifting the graph two units to the right. Here’s what the transformed graph looks like:
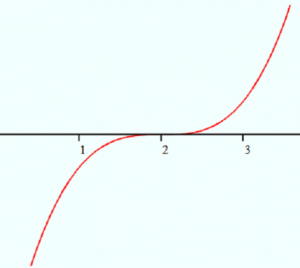
Step 3: Write the equation. For any function, f(x), the graph of f(x + c) is the graph shifted to the left and the graph of f(x – c) is the graph shifted to the right. The question asks for two units (i.e. 2) to the right, so the final equation is f(x) = (x – 2)3.
Caution: the graph of x2 – 2 moves the graph down two units, not right!
Example problem 2: Sketch the graph of x2 + 2.
Step 1: Visualize the graph of x2.
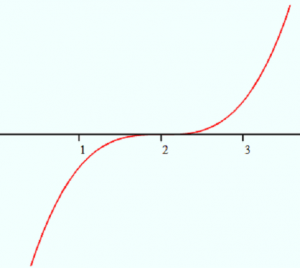
Step 2: Sketch the graph. For any function, f(x), a graph f(x) + c is the graph shifted up the y-axis and a graph f(x) – c is a graph shifted down the y-axis. Therefore, x2 + 2 is the graph of x2 shifted two units up the y-axis.
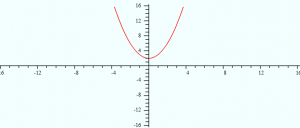
That’s it!
Tip: You can also flip graphs on the x-axis by adding a negative coefficient. For example, while x2 is a parabola above the x-axis, -x2 is a mirror image over the x-axis.
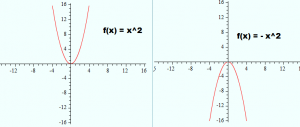
Other Transformations
A Box Cox transformation is used when you need to meet the assumption of normality for a statistical test or procedure. It transform non-normal dependent variables into a bell shape.
Another way to normalize data is to use the Tukey ladder of powers (sometimes called the Bulging Rule), which can change the shape of a skewed distribution so that it becomes normal or nearly-normal. A third, related procedure, is a Fisher Z-Transformation. The Fisher Z transforms the sampling distribution of Pearson’s r (i.e. the correlation coefficient) so that it becomes normally distributed.
Generalized Procrustes analysis, which compares two shapes in Factor Analysis, uses geometric transformations (i.e. rescaling, reflection, rotation, or shift) of matrices to compare the sets of data. The following image shows a series of transformations onto a green target triangle.
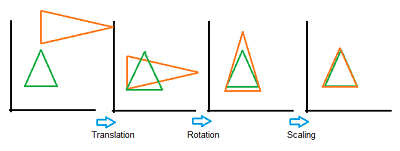
References
Cox, N. (2005). Transformations: An Introduction. Retrieved February 25, 2018 from: http://fmwww.bc.edu/repec/bocode/t/transint.html
Coxeter, H. et. al (1967). Geometry Revisited. Washington, DC: Math. Assoc. Amer., p. 80.
Croft, H.et al. (1991). Unsolved Problems in Geometry. New York: Springer-Verlag, p. 3.
Gray, A. (1997). “Isometries and Conformal Maps of Surfaces.” §15.2 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 346-351.
Revision Maths. Geometry and Measures: GCSE Maths. Retrieved from https://revisionmaths.com/gcse-maths-revision/shape-and-space/transformations on August 19, 2019
Peil,Timothy. Survey of Geometry.
Retrieved from http://web.mnstate.edu/peil/geometry/C3Transform/2isometry.htm on December 30, 2018.
Do, Norman. Symmetry in Geometry. Retrieved from http://users.monash.edu/~normd/documents/MATH-348-lecture-21.pdf on December 30, 2018.
What is a Horizontal Shift of a Function?
A horizontal shift adds or subtracts a constant to or from every x-value, leaving the y-coordinate unchanged. The basic rules for shifting a function along a horizontal (x) are:
Rules for Horizontal Shift of a Function
Compared to a base graph of f(x),
- y = f(x + h) shifts h units to the left,
- y = f(x – h) shifts h units to the right,
Where h > 0.
Look carefully at what the positive or negative added value h is doing: it’s the opposite of what you might expect. Positive values of h shift in the negative direction along the number line and negative h values shift the positive direction.
Example of a Horizontal Shift
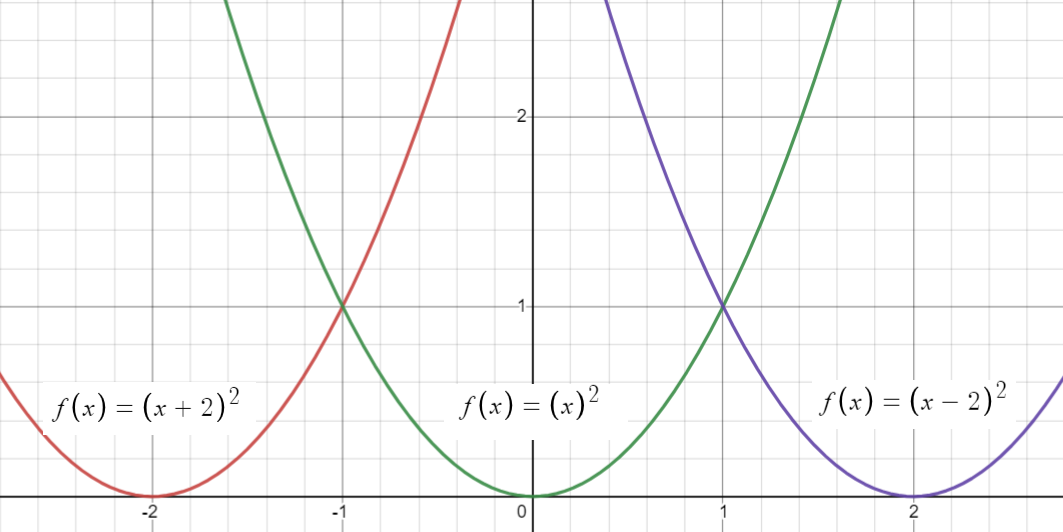
A horizontal shift of the function f(x) = x2 of 2 units (i.e. h = 2) results in:
- f(x) = x2 + 3 (3 units to the left),
- f(x) = x2 + 3 (3 units to the right)
The following graph shows the base function f(x) = x2 and the two “new” graphs created when we added 2 or subtracted 2.
Example Questions
Example question #1: How are the graphs of y = √(x) and y = √(x + 1) related?
Solution:
Step 1: Compare the right sides of both equations and note any differences:
- √(x)
- √(x + 1)
The difference between the equations is a “+ 1”.
Step 2: Choose a rule based on whether Step 1 was positive or negative:
Step 1 for this example was positive (+ 1), so that’s rule 1:
y = f(x + h) shifts h units to the left
Step 3: Place your base function (from the question) into the rule, in place of “x”:
y = f(√(x) + h) shifts h units to the left
Step 4: Place “h” — the difference you found in Step 1 — into the rule from Step 3:
y = f(√(x) + 2) shifts 2 units to the left
That’s it!
Example question #2: The following graph shows how the average cost of a new car tire compares from Jacksonville, Florida (red) to Miami, Florida (Blue). Write a formula for the transformation of g (blue graph) to f (red graph).
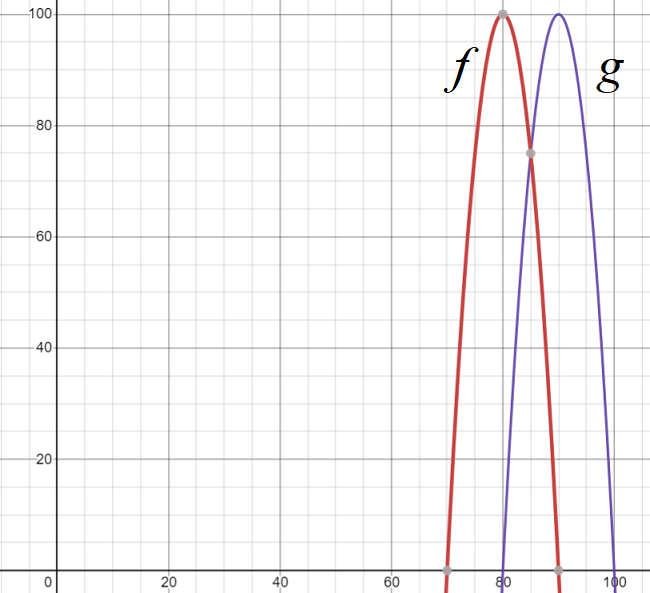
Solution: The graph g shifts 10 units to the right of f, so:
g(x) = f(x – 20) .
If you’re not sure about how I arrived at this formula, the following few steps break it down into simple parts:
Step 1: Decide which direction the graph is traveling (left, or right?). The question asks is for a formula for the transformation of g (blue graph) as a transformation of f (red graph). In other words, what direction do we need to travel to turn f into g? A look at the graph shows that moves to the right.
Step 2: Take your answer from Step 1 and then refer to the rules to tell you whether it’s a positive or negative shift.
Rule 2 states:
y = f(x – h) shifts h units to the right.
That means moving to the right must mean we have a “-” shift.
Put this value aside for a moment.
Step 3: Locate two x-values on the horizontal axis: one for each graph:
- g (blue graph) = 70
- f (red graph) = 90.
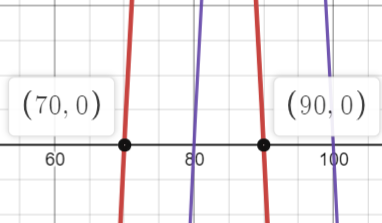
Step 4: Subtract the lowest number in Step 3 from the highest:
90 – 70 = 20.
Step 5: Combine your answers from Steps 2 and 4:
– 20.
Step 6: Place your answer from Step 5 into the rule you chose in Step 2, replacing the “h” with your value (- 20 in this example):
g(x) = f(x – 20)
Don’t forget to rename the formula with the one given in the question!
References
Graph created with Desmos.com.