Rationalizing substitutions involves turning a function that isn’t a rational function into a one that is. This allows you to integrate by a specific type of u substitution.
When to Use Rationalizing Substitutions
A rational function is a ratio of two polynomials. Polynomials cannot have:
- Fractional exponents, like x½
- Negative exponents, like x-2
- Variables within the radical (square root) sign. For example, √2.
- Division by a variable.
If you see any of the above in your “rational” function, it may look like a rational function, but it actually isn’t. In these cases, you can use the method of rationalizing substitutions, which essentially turns a rational-looking function into a proper rational function.
Rationalizing Substitutions: Example
The following short video shows you how to solve the above integral using rationalizing substitutions. Or, you can download this PDF of solutions, which was generated at Symbolab. See below for instructions on how to use that online calculator.
Symbolab Calculator Option
If algebra isn’t your forte, you really can’t beat the online calculator at Symbolab. It shows all the steps in the above video, plus you can download a PDF of all the steps! To use the online integral calculator:
Step 1: Go to https://www.symbolab.com/solver/integral-calculator/.
Step 2: Place your cursor before the integral symbol and click the “partial fractions” button (the partial fractions method is the one used in the video).
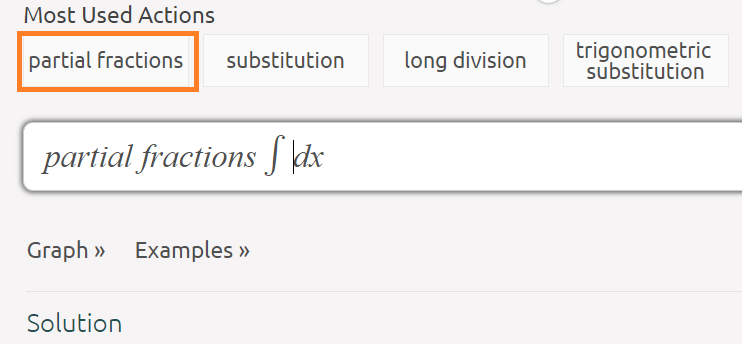
Step 3: Type in your function. For this example, I had to use the square root button (blue) and nth root button (orange):
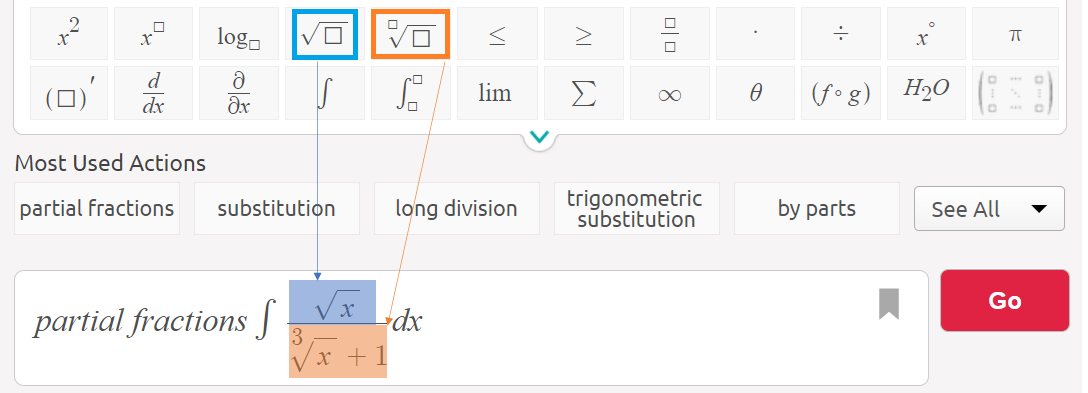
Step 4: Click the red GO button.
Step 5: Print your solutions or download a PDF.