Analytic geometry creates a connection between graphs and equations. For example, the linear function f(x) = x2 – 2 (an equation) can also be represented by a graph:
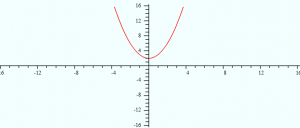
Euclidean Geometry is based solely on geometric axioms without formulas or co-ordinates; Analytic geometry is the “marriage” of algebra and geometry with axes and co-ordinates [1].
Calculus and Analytic Geometry
Calculus and analytic geometry have become so intertwined, it’s rare nowadays to find a course in pure “Analytic Geometry”. It’s more common to take a course in Calculus and Analytic Geometry, which blends the principles of basic analytic geometry with concepts like functions, limits, continuity, derivatives, antiderivatives, and definite integrals.
Topics in Analytic Geometry A to Z
- Arc Length Formula: An “arc” is a curve segment; The arc length formula tells you how long this segment is.
- Area of a Bounded Region: are of a shape contained within a set of functions.
- Area under the curve: Calculating the area between a graph and the x-axis.
- Centroid: The average of all points in an object (e.g. the center of volume or mass).
- Bipolar Coordinate System: An unusual system used in GIS and electrical field theory.
- Center function: gives the trilinear coordinates of a triangle’s center.
- Coterminal Angles: Angles that have the same terminal side.
- Distance Formula / Function: measures the distance between two points in a set (e.g. on a line).
- Delta x / Delta y: Distance traveled along the x- or y-axis.
- Displacement Function: gives us how far a particle has moved from a starting point at an given time.
- Distance Traveled (using derivatives).
- Double Angle Formulas: Sin, Cos, Tan
- Epicycles of Ptolemy: A ancient model of the universe.
- Hyperbola: Two symmetrical curves that have special properties.
- Intersection of lines: The place where two or more graphs cross each other.
- Length of a Line Segment: Measuring “how far” along an x or y axis.
- Level Curve: Analogous to contour lines on a map.
- Parabola: a u-shaped curve; The graph of a quadratic function.
- Parallel Cross Sections: repeated cross sections for a solid, parallel to each other.
- Pedal Coordinates: Tangential coordinates.
- Polar coordinates: “Circular” coordinates on a plane.
- Rate of change: a measure (a rate) of how things are changing.
- Slope: the ratio of a change in x (δx) to a change in y (δy).
- Quadrant: one of the four regions of the Cartesian plane / x-y axis.
- Riemann Sums: Estimating the area under a curve with rectangles.
- Secant line: A secant line connects two ore more points on a curve; An external secant is the “outside” part of the secant line.
- Sketching Graphs on the Cartesian Plane.
- Special Curves: Definition, Examples
- Spherical coordinates: Coordinate system on a sphere.
- Tangent line: a line that touches a graph at only one point and is practically parallel. See also: Vertical Tangents and Horizontal Tangents.
- Tautochrone Problem / Brachistochrone: Classic problems about swinging pendulums.
- Testing for Symmetry of a Function.
- Transformations: shifts, dilations and other “movement” along the x or y axis.
- Trilinear Coordinates: a way to represent a point in the plane using a triangle as the coordinate system.
- Vectors: show magnitude and direction.
- Velocity: Rate of change of displacement.
- x, y coordinate system: A system with a horizontal (x) axis and vertical (y) axis.
- x and y intercepts: The points where a graph crosses the x-axis or y-axis.
- X Y Plane
Curves:
- Equiangular Spiral, Spira Mirabilis (Logarithmic Spiral)
- Lamé curve
- Quadric Surface: Equations, Examples
X Y Plane
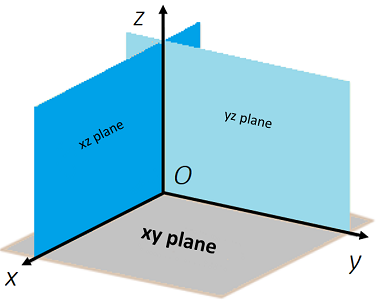
In 3D space (also called xyz space), the xy plane contains the x-axis and y-axis:
The xy plane can be described as the set of all points (x, y, z) where z = 0. In other words, any point (x, y, 0). For example, all of the following points are on the xy plane:
- (1, 5, 0)
- (-2, 19, 0)
- (π, -1, 0)
- (.5, .2, 0)
This fact gives us the equation for the xy plane: z = 0.
This is just an extension of the same idea of the x-axis (in the Cartesian plane) being the place where y = 0:
The xy plane, together with the yz plane and xz plane, divide space into eight octants. The O in the center of the diagram is the origin, which is a starting point for the 3D-coordinate system. The points are described by an ordered triple of real numbers (x, y, z). For example, the point (2, 3, 0) can be found at:
- x = 2,
- y = 3,
- z = 0.
As z is zero, we know this point must be somewhere on the xy plane.
Distance Formula for Points in the XY Plane
The distance between any two points in xyz-space can be found with a generalization of the distance formula:
![]()
Example question: What is the distance between the points (4, 3, 0) and (2, 9, 0)?
Step 1: Identify the coordinate components that we need to put into the formula. We know our coordinates are always ordered (x, y, z), so:
- (4, 3, 0):
- x1 = 4
- y1 = 3
- z1 = 0.
- (2, 9, 0):
- x2 = 2
- y2 = 9
- zz = 0.
Don’t worry about which coordinate is which (e.g. does x = 4 go into x1 or x2?). The distance formula squares these values, so you’ll get the same answer no matter which way you choose.
Step 2: Plug your values from Step 1 into the distance formula:
![]()
If you aren’t good with algebra, head over to Symbolab and just replace the x, y, z values with your inputs.
Quadric Surface
A quadric surface is a 3D extension of a conic (ellipsis, hyperbola, or parabola). In 2D space, they are defined by quadratic equations in 2D space [2]. Quadric refers to the degree of the equation describing the surface: variables in these equations are raised to the 2nd power. They can be described, in general, as a graph of an equation expressed in the form [3]:
Ax2 + B2 + C2 + Dxy + Exz + Fyz + Hx + Iy + Jz + K = 0.
Where A, B, C, D, E, F, H, I, J, K are fixed constants and x, y, z, are variables.
Different types of quadric surfaces can be obtained from simplifying this equation by rotations and translations of the x, y, z coordinate axes.

Types of Quadric Surfaces
There are six basic types of quadric surface [2]:
- Ellipsoid,
- Elliptic paraboloids,
- Hyperbolic paraboloid,
- Cones,
- Hyperboloids of one sheet,
- Hyperboloids of two sheets.
Other examples of quadratic surfaces include the cylinder, elliptic cone, elliptic cylinder, elliptic hyperboloid, hyperbolic cylinder, paraboloid, sphere, and spheroid.
1. Ellipsoid
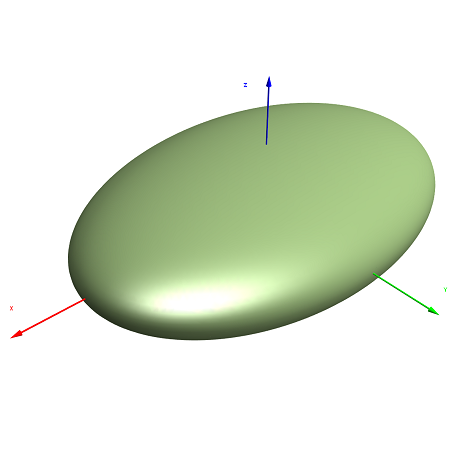
The general equation for an ellipsoid is:
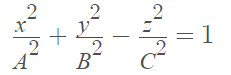
If A = B = C, the shape is a sphere.
2. Elliptic paraboloids
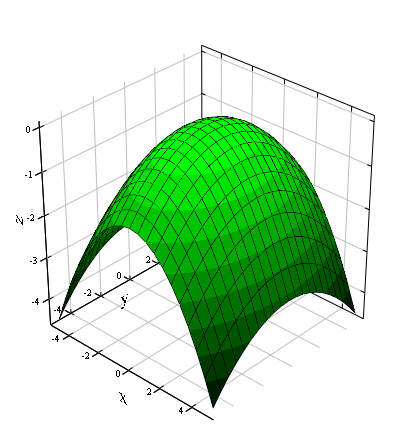
The equation for an elliptic paraboloid is:
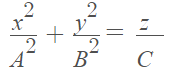
Elliptic paraboloids have ellipses as cross sections. If A = B, the cross section is a circle.
3. Hyperbolic paraboloid
The equation for a hyperbolic paraboloid is:
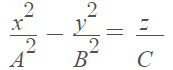
Hyperbolic paraboloids are saddle-shaped, like a Pringle. The sign of c determines whether the graph opens up or down. A positive value for c has the saddle right side up (as if it were being placed on a horse).
4. Cones
The equation for a cone is [4]:
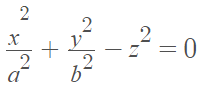
5. Hyperboloids of one sheet
The equation for the hyperboloid of one sheet is:
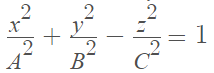
6. Hyperboloids of two sheets
The equation for the hyperboloid of two sheets is:
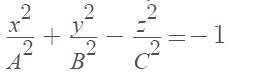
References
[1] Analytic Geometry and Calculus. Retrieved May 3, 2021 from: math.uci.edu/~ndonalds/math184/analytic.pdf
[2] Quadric Surfaces. Retrieved July 31, 2021 from: https://web.cs.wpi.edu/~matt/courses/cs563/talks/renderman/quadric.html
[3] Quadric Surfaces. Retrieved August 1, 2021 from: https://opentextbc.ca/calculusv3openstax/chapter/quadric-surfaces/
[4] Quadratic Surfaces. Retrieved August 8, 2021 from: http://www.staff.city.ac.uk/o.castro-alvaredo/teaching/surfaces.pdf