Watch the video for two examples of how to find total distance traveled in calculus—on an interval [0, 5]— or read on below:
Contents (Click to skip to that section):
- How to Find Total Distance
- Distance From a Point To a Line
- Total Distance vs. Total Displacement
- How to Find Total Displacement
How to Find Total Distance
Most distance problems in calculus give you the velocity function, which is the derivative of the position function. The velocity formula is normally presented as a quadratic equation.
You can find total distance in two different ways: with derivatives, or by integrating the velocity function over the given interval.
How to Find Total Distance with Derivatives
Example problem: Find the total distance traveled for a particle traveling in a horizontal motion from t = 0 to t = 5 seconds according to the position function:
s(t) = 8t2 – 4t.
Step 1: Find the velocity function. The velocity function is the derivative of the position function. So, to find the velocity function you need to differentiate s(t) = 4t2 – 2t, using the power rule and derivative of a constant rule:
v(t) = 16t – 4
Step 2: Set the velocity function to zero, then solve, to find where the velocity function changes direction:
- v(t) = 16t – 4 = 0
- 16t – 4 (+ 4) = 0 (+ 4)
- 16t(/16) = 4 (/16)
- t = 4/16 = 1/4
Note: Alternatively, you could graph your velocity function and note where areas of the graph are above or below the x-axis. This where the velocity as a vector has changed direction.
Step 3: Solve the position function for the starting and ending interval values (which are 0 and 5, according to the question), and any t-values you found in step 2:
- s(0) = 8(0)2 – 4(0) = 0.
- s(1/4) = 8(¼)2 – 4(1/4) = -½
- s(5) = 8(5)2 – 4(5) = 180.
This gives you the position of the object at each time interval.
Step 4: Find the distance traveled between each point. These are vectors, so we have to use absolute values to find the distance:
- Between 0 and -½, distance = |-½ – 0| = ½
- Between -½ and 180, distance = |180 – (-½)| = 180½
Step 5: Add your values from Step 4 together to find the total distance traveled.
½ + 180 ½ = 181
How to Find Total Distance: Integrals
Example question: A particle travels according to the following velocity function:
v(t) = 3t2 – 12.
What is the total distance traveled from t = 1 to t = 3?
Step 1: Set the velocity equal to zero to find where the function changes direction:
- v(t) = 3t2 – 12 = 0
- 3(t2 – 4) = 0 (factoring out).
- 3(t – 2)(t + 2) = 0
- t = -2, +2
We’re working with the closed interval [1, 3] (from the question), so the point we’re interested in (the one that falls in the interval) is t = 2.
Step 2: Integrate the velocity function for each interval. To solve, you need two separate definite integrals:
- From the starting point (t = 1) to zero (t = 2),
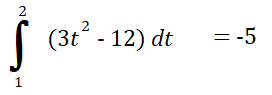
- From the zero (t = 2) to the ending point (t = 3).
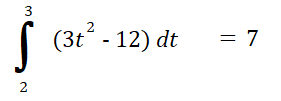
Step 3: Add the absolute values of the amounts you calculated in Step 2:
5 + 7 = 12.
The total distance traveled is 12 units.
Calculating the Distance From a Point To a Line
The distance from a point to a line is the length of the shortest path between that point and the place on the line nearest to it. This path is always the line that is perpendicular (at right angles) to your original line.
1. If you know the coordinates
If you know the Cartesian coordinates of your point and you have an equation for your line, you can calculate the distance between the point and the line with the formula:
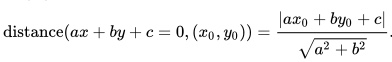
Where:
- x0, y0 are the coordinates of the point,
- a, b, and c are the coefficients (and constant) for the line a x + b y + c = 0.
Example
Suppose your line was given by 4 x + y = 0, and your point was (2, 2).
As you have coordinates, you can use the first equation given above.
The distance from the point to the line would be:
|4 · 2 + 1 · 2 | / √(4+ 4).
This is equivalent to |10|/(2 √2), or approximately 3.54.
2. If you don’t have coordinates
Sometimes you don’t have an equation for the line. If all you know about your line is two points that it crosses, you can use another formula to calculate that distance between a point and the line. Let’s make our point x0, y0 again, and define the point as one which goes through x1, y1 and x2, y2 . Then the distance is given by
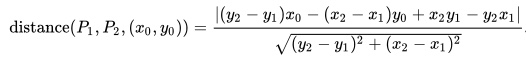 .
.
These formulas can be proved through algebra, through geometry,and through vector analysis.
Total Distance vs. Total Displacement
The definite integral of the velocity function of an object gives you the total displacement—how far an object is from a point of origin. However, this is different from distance traveled. Let’s say you were going to the local market, which is about 1 mile from your house. The total displacement, when you reach your destination, is 1 mile. When you get home, your total displacement is zero (you’re back at your starting point). But the distance traveled is 2 miles: one mile to the market, and one mile back again. Displacement doesn’t reflect distance traveled.
If an object is traveling in one direction (e.g. along the x-axis), without reversing or changing course, then total distance is the same as total displacement.
How to Find Total Displacement
The formula for total displacement is:
![]()
Where:
- Σ = summation notation (add everything up)
- Δxi are the individual displacements.
Example question: A car travels 2 miles E then 4 miles W. What is the total displacement?
Solution:
At this stage, it may help to draw a graph of the problem. Here’s what we are trying to find in this question:
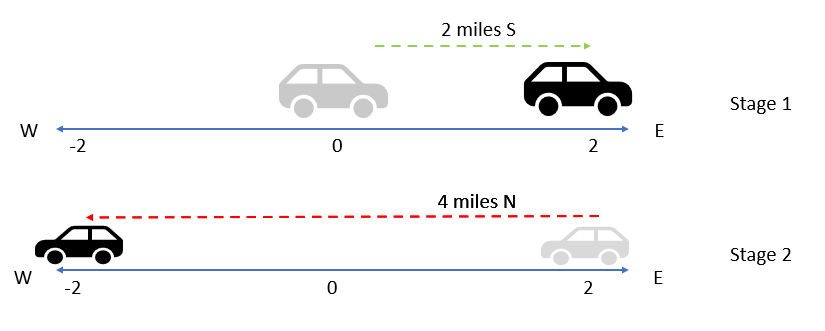 The picture shows that the car is -2 miles from its starting position. We can prove that mathematically with the formula.
The picture shows that the car is -2 miles from its starting position. We can prove that mathematically with the formula.
Step 1: Calculate the individual displacements (Δxi) using the displacement formula:
Δx = xf – x0
Where:
- xf = final position,
- x0 = starting position.
For this question we have two individual displacements: 2 miles E and 4 miles W.
- 2 miles E: We started at position “0” and ended at “2”, so:
Δx = 2 – 0 = 2 - 2 miles S: We started at “2” and ended at -2, so:
Δx = -2 – (2) = -4
Step 2: Add up the individual displacements you calculated in Step 1:
2 + (-4) = -2.
That’s it!
References
Gore, Bhalchandra. On Finding the Shortest Distance from a Point to a Line. Retrieved from
https://www.ias.ac.in/article/fulltext/reso/022/07/0705-0714 on December 15, 2018.
Distances. Math 21a, Fall 2008. Retrieved from http://www.math.harvard.edu/archive/21a_fall_08/handouts/distances/distance.pdf on December 15, 2018.
Larson, R. (2011). Calculus 1 with Precalculus. Cengage Learning; 3 edition.