Contents:
- Definition
- Constant of Integration: Why add a (+C)?
- Indefinite Integral Rules:
See also:
Integration by parts
Net change Theorem
What is an Indefinite Integral?
Indefinite Integrals (also called antiderivatives) do not have limits/bounds of integration, while definite integrals do have bounds.

Indefinite Integral and The Constant of Integration (+C)
When you find an indefinite integral, you always add a “+ C” (called the constant of integration) to the solution. That’s because you can have many solutions, all of which are the set of all vertical transformations of the antiderivative.
For example, the antiderivative of 2x is x2 + C, where C is a constant. The derivative of a constant is zero, so C can be any constant, positive or negative. Four antiderivatives of 2x are x2 + 1, x2 -1, x2 + 2 or x2 – 2.
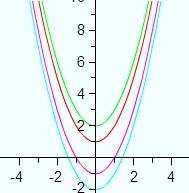
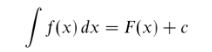
To put that another way, an indefinite integral doesn’t have any limits, so you’re finding a set of integrals (rather than just one specific one). The “+ C” indicates that the solution actually has infinite possibilities.
If this sounds strange, you’ve actually been using a similar technique in algebra, when you put in a k for a constant (e.g. f(x) = k * sin(x)): you’re letting the reader know that there’s a wide variety of possible values.
Another way to look at it: The “C” represents uncertainty in your solution.
Why is The Constant of Integration Necessary for an Indefinite Integral?
To answer that question, let’s take a look at a basic function:
f(x) = 3x2
Let’s assume that this is the answer to an integration problem. Integration is the reverse of differentiation (that’s why indefinite integrals are also called antiderivatives), so you’re trying to find a function F(x) that has a first derivative of 3x2:
F′(x) = 3x2
What function has a first derivative of 3x2? One solution is x3. Using the rule for differentiating exponents, we get
- 3x(3 – 1)
- 3x2
But that isn’t the only solution. Adding a constant to the solution doesn’t change it in any way, because the derivative of a constant equals zero. In other words, you could have an infinite number of solutions, like:
- 3x2 + 9
- 3x2 + .09
- 3x2 + π
- 3x2+ 3/2
- 3x2 – 8629862394629834
- 3x2 – 9
As it’s impossible to write out all of the infinite solutions, we just put in a constant of integration as a placeholder and say 3x2 + C.
Constant Difference Theorem
The example above showed that multiple derivatives of the same function differ only by one constant, C, which could equal zero. The constant difference theorem uses this fact, along with the difference of two functions:
If f and g are differentiable on an interval, and if f′(x) = g′(x) for all x in that interval, then f – g is constant on the interval; that is, there is a constant k such that f(x) – g(x) = k, or equivalently,
f(x) = g(x) + k
for all x in the interval. (Anton et al. 2012).
Indefinite Integral Rules
Indefinite integrals may or may not exist, but when they do, there are some general rules you can follow to simplify the integration procedure.
Common Indefinite Integral Rules
∫m dx = mx + c, for any number m.
∫xn dx = 1⁄n + 1xx + 1+ c, if n ≠ –1.
∫1⁄xdx = ln |x| + c, for x ≠ 0.
∫sin x dx = −cos x + c
∫cos x dx = sin x + c
∫ex dx = ex + c
The Sum Rule
The integral of the sum of two functions is the sum of their separate integrals:
Addition: ∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx
Subtraction: ∫[f(x) − g(x)]dx = ∫f(x)dx − ∫g(x)dx
Note though, that this rule doesn’t tell you how to find the individual integrals. For that, you’ll have to refer to function specific rules (like the integral rule or trigonometric rules).
Example problem: Find ∫ cos x + x dx
- Separate the integrals: ∫cos x + x dx = ∫cos x dx + ∫x dx
- Find the individual solutions:
- ∫cos x = sin x
- ∫x = = sin x + x2/2 + C (see: power function integration rule)
-
Solution = sin x + x2/2 + C
See: Sum Rule: Definition and Examples for a couple of step by step examples.
The Multiplication Rule
Any constant factor can be moved outside of the integration symbol:
∫ax ndx = a∫xn dx for any constant ‘a’.
Similarly,
∫[af(u) + bg(u)]du = a = ∫ f(u) du + b ∫g(u) du
Linear Substitution
If F′(x) = f(x) then for any m ≠ 0,
∫f(mx + b)dx = 1⁄mF(mx + b) + c
Indefinite Integrals for Trigonometric Identities
∫ cos x dx = sin x + C
∫ sin x = -cos x + C
∫ sec2 x dx
∫ csc2 x dx = -cot x + C
∫ sec x tan x dx
∫ csc x cost x dx
Indefinite Integrals of power functions
The following general rule is for integrating power functions of the form
f(x) = xn(n ≠- 1):
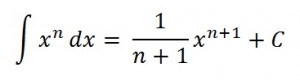
It’s actually easier than it looks—all the formula is saying is to add one to the power, divide by that power, and then add a “C” for constant.
Example Problems:
Example Problem #1: Find the antiderivative (indefinite integral) for 20x3
Step 1: Increase the power by 1:
20x3 = 20x4
Step 2: Divide by the new power you calculated in Step 1:
20x4 = 20⁄4 x4 = 5x4
Step 3: Add “C”:
5x4 + C
Example Problem #2: Find the antiderivative (indefinite integral) for 3x8
Step 1: Increase the power by 1:
3x8 = 3x9
Step 2: Divide by the new power you calculated in Step 1:
3⁄9x9 = 1⁄3x9
Step 3: Add “C”:
1⁄3x9 + C
Example Problem #3: Find the antiderivative (indefinite integral) for x4 + 6
Step 1: Increase the power by 1 for x (note that you add x0 to a constant on its own — in this case, 6 becomes 6x0).
x4 + 6x0 = x5 + 6x1
Step 2: Divide by the new powers you calculated in Step 1:
x5⁄5 + 6x1⁄1 = 1⁄5x5 + 6x1
Step 3: Add “C”:
1⁄5x5 + 6x1 + C
That’s it!
Tip: When adding 1 to your power, remember that x becomes x1, and a constant becomes that constant plus x0. For example, 6x10 + 17x + 9 becomes 6x10 + 17x1 + 9x0 before you add the power and 6x11 + 17x2 + 9x1 after you add the one.
Back to top
Other References
Anton, H. et al. (2012). Calculus Single Variable. Wiley.
Riley, K. et al. (2006). Mathematical Methods for Physics and Engineering. A Comprehensive Guide. Cambridge University Press
Handbook of Mathematical Formulas and Integrals