An external secant segment is the part of a secant line lying outside a circle.
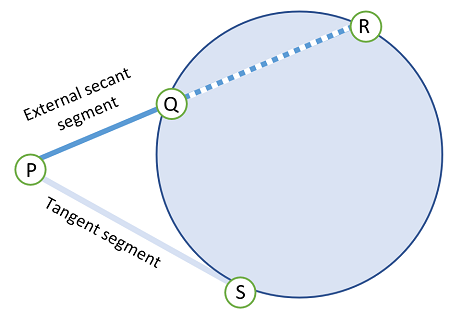
The Exsecant function is used to find the length of the external secant segment.
Finding Unknown Lengths with External Secant Segment
The following ratio allows you to solve for unknown lengths of secant lines, external secant segments, or internal segments (the parts of secant lines that are inside the circle):
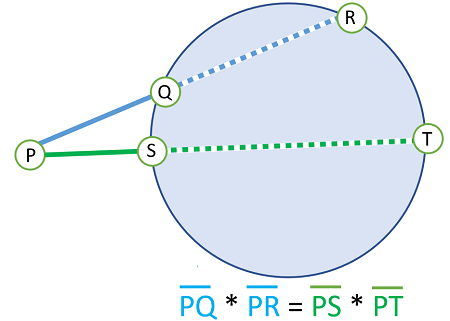
This relationship is formally called Steiner’s Theorem [1] can be stated in words as: If two secant segments are drawn from an external point to a circle, then the products of the lengths of each secant line with its external segment are equal.
The theorem is rarely called by its proper name, perhaps to avoid confusion with the other Steiner’s Theorem which is used in physics to determine moments of inertia.
Proof of Steiner’s Theorem
Example question: Prove that PQ * PR = PS * PT.
Step 1: Draw RS and QT:
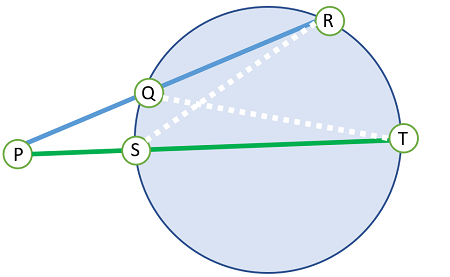
From this image, you can deduce that ∠R and ∠T are congruent* because they intersect the same arc (the arc between points Q and S):
∠R ≅ ∠T
*Congruent objects have the same shape and dimensions.
Step 2: Write that ∠P is congruent to itself; This is because of the reflexive property of congruence (which simply states that any shape is congruent to itself). This is an obvious step, but it’s needed in a formal proof. So we have:
∠P ≅ ∠P.
Step 3: State that two triangles △PRS and △PQT are equivalent. This follows from Steps 1 and 2 plus the AA similarity theorem which states that two triangles are similar if two pairs of angles are congruent. In other words, we proved that two angles in Steps 1 and 2 are congruent, so the third angle must be congruent as well:
△PRS ~ △PQT
Step 4: Derive the cross product of side lengths. Since we have proved that the two triangles are similar in Step 3, the side lengths must be proportional:
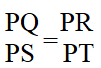
We can rewrite this with the Cross Product Property:
PQ * PR = PS * PT.
That’s it!
References
[1] Jones, J. Steiner’s Theorem. Retrieved April 15, 2021 from: http://jwilson.coe.uga.edu/EMT669/Student.Folders/Jones.June/steiner/steinerthm.html