There are several different ways to define a bipolar coordinate system. Two of the most common are Grubert’s bipolar system and the bipolar system of two concentric circles.
Grubert’s Bipolar System
The bipolar coordinate system, created by Grubert in 1859 [1], is an unusual coordinate system where coordinates of a point are its distance from two poles, or fixed points. In other words, it’s a system with two points that are a specified distance apart, where a point’s coordinates are the its distance from the two points, A plus or minus indicates which side of the line joining the two poles the point is [2].
It is sometimes called a dipolar, biradial, vectorial, or bivectorial system.
Bipolar Coordinate System: Concentric Circles
An alternate definition of a bipolar coordinate system is one where two concentric families of circles share two common center points; the bipolar coordinates of a point are the values of two parameters defining the concentric circles. The distance between the two center points, or foci, is usually a constant 2a, but may be variable in some cases (e.g., the van der Grinten map projection) [2].
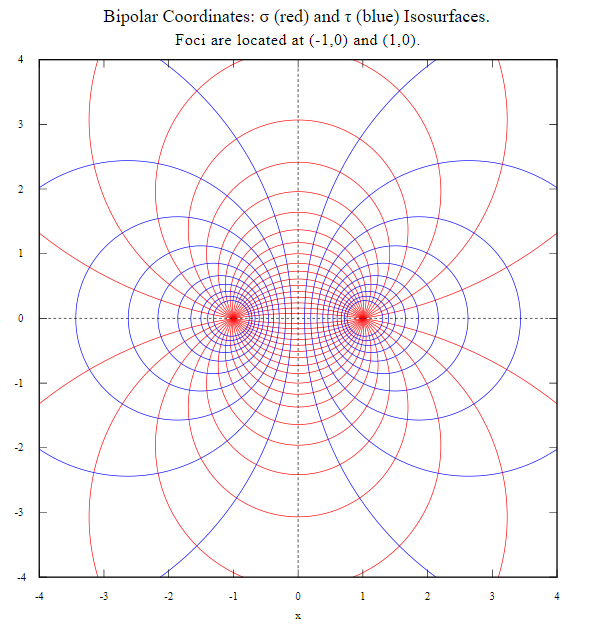
The formula, which describes how τ and σ are connected with the Cartesian coordinates x and y, is:
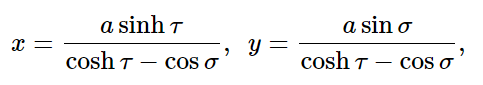
Where 0 ≤ σ < π, -∞ < τ < ∞.
The bipolar coordinate system has two rotational forms, toroidal and bispherical [3].
What is the Bipolar Coordinate System Used For?
The Bipolar Coordinate System has a range of applications, including providing an unambiguous localization of points in a 3D space [4]. Practical applications include [5]:
- Lines of flux for an electric dipole,
- Electric fields between two spheres,
- Parallel microwave transmission lines.
While the system is sometimes helpful, it isn’t easy to work with. Mark Wagner states in The Geometries of Visual Space that it is “awkward to use at best” [6].
References
Image: Mkwadee,
[1] Wood, F. Coordinate Systems in One and Two Dimensions. Retrieved January 19, 2022 from: https://kuscholarworks.ku.edu/bitstream/handle/1808/14967/Wood_Coordinate_Systems%20(Smaller).pdf;jsessionid=2550A8539FB17CD6E492C09B5C0CCF4E?sequence=1
[2] American Society of Civil Engineers. (1994). Glossary of the Mapping Sciences.
[3] Arfken (1970). Chapter 1.
[4] Wade, G. (2012). Acoustical Holography
Volume 4 Proceedings of the Fourth International Symposium on Acoustical Holography, Held in Santa Barbara, California, April 10–12, 1972.
[5] Westgard, J. (2012). Electrodynamics: A Concise Introduction. Springer New York.
[6] Wagner, M. (2012). The Geometries of Visual Space. Taylor & Francis.