Coterminal angles have the same terminal sides: they start and end in the same place. For example, θ = 140° and Β = -220° are coterminal angles:
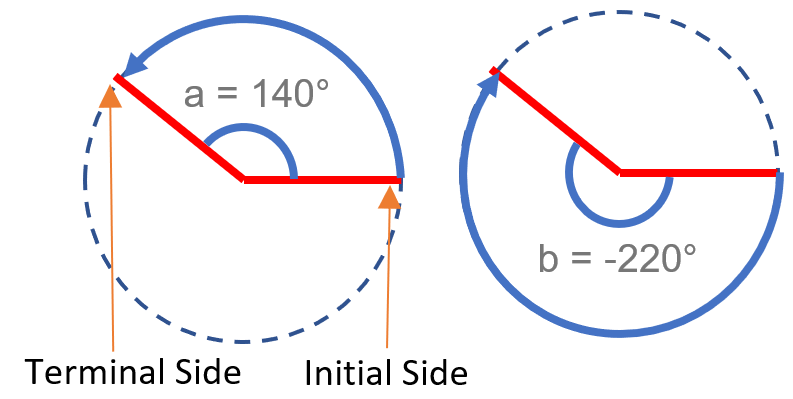
How to Find Coterminal Angles
The difference between two coterminal angles is a multiple of 360° or 2π radians, because if the terminal side rotates 360° (or, equivalently, 2π radians) that’s one complete revolution of the circle to the same location. So, one way to find these angles is to add (or subtract) multiples of 360°. For example, let’s say you had 660°. Two coterminal angles are:
- 660° + 360° = 1020°
- 1020° + 360° = 1380°
Example question #1: Find a positive and a negative coterminal angle for 560°.
Step 1: To find a positive angle, add 360°:
560° + 360° = 920°
Step 2: To find a negative angle, subtract 360°:
560° – 360° = 200°
This isn’t negative yet, so we’ll keep going:
200° – 360° = -160°
Example question #2: Find a positive and a negative coterminal angle for π/6;.
Step 1: To find a positive angle, add 2π:
π/6 + 2π = 13π/6
Step 2: To find a negative angle, subtract 2π:
π/6 – 2π = -11π/6
Using Coterminal Angles to Find Function Values
For trigonometric functions, coterminal angles have the same function value; That’s because the function repeats itself over and over: the space in between the angles is a multiple of a trigonometric function’s period. Add or subtract a period, and you’ll get a coterminal angle. We can use this information to evaluate trig functions.
Example Question #1: Evaluate cos 780°
Step 1: Express the function in terms of an angle between 0° and 360°:
- 780° = cos(780° – 2· 360°)
- = cos 60°
- = ½
That’s it!
This next question uses a reference angle. A reference angle is the positive acute angle made by the terminal side of the angle and the x-axis [1].
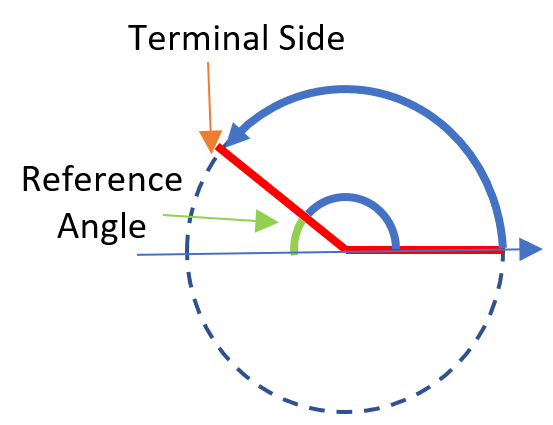
The value of any trigonometric function for any angle θ is equal to the function value for the reference angle, except possibly for a change of sign.
Example Question #2: Evaluate cot(–405°).
Step 1: Express the function in terms of an angle between 0° and 360°:
- cot(-405deg;) = cot(-405deg; + 2 · 360deg;) = cot 315deg;.
The angle 315° is in quadrant 4; its reference angle is -45deg;, so:
- cot 315deg; = -45° = -1
That’s it!
References
Lial, M. et,al. (2013). Trigonometry. Pearson Education.