An ellipsoid is a three-dimensional shape that has an ellipse or circle for every cross section. A sphere is a special case, but every ellipsoid is symmetric about three mutually perpendicular axes which meet in its center.
Equations and Types of Ellipsoid
Let a, b, and c be positive real numbers which represent the length of the principal semi-axes, measured at x, y, and z respectively. Then we can write the general equation of an ellipsoid as 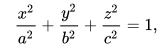
For this shape, the points (a, 0, 0), (0,b,0) and (0,0,c) will lie on the surface. If a = b = c, we have a sphere. If two of the axes are equal and the third is different, we call the shape a spheroid or an ellipsoid of revolution. We can create an ellipsoid of revolution by revolving an ellipse about one of its axes. If the two equal axes are greater than the third, we can say that our spheroid is oblate. If the two equal axes are less than the third, we say it is prolate. Below is an image of three types of ellipsoids.
- The first is a sphere, with a = b = c.
- The next is an oblate spheroid; a and b are greater than c.
- The third we call tri-axial; the three axes are all different.

Applications
Although it was thought that the earth was a sphere, Isaac Newton predicted, based on its orbit, that it was, in fact, an ellipsoid. He was very nearly correct: it is now universally understood that it is, in fact, a geoid that can be nearly approximated by a flattened sphere. This approximation is called the reference ellipsoid. The equatorial axis of this shape is about 21 kilometers longer than the polar axis.
References
Image: Ag2gaeh [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)] Osserman, Robert. Geometry. Encyclopædia Britannica. Date Published: August 25, 2006 Retrieved from https://www.britannica.com/science/ellipsoid on April 19, 2019 Nature of Geographic Information, Chapter 4. Retrieved from https://www.e-education.psu.edu/natureofgeoinfo/c2_p15.html on April 20, 2019