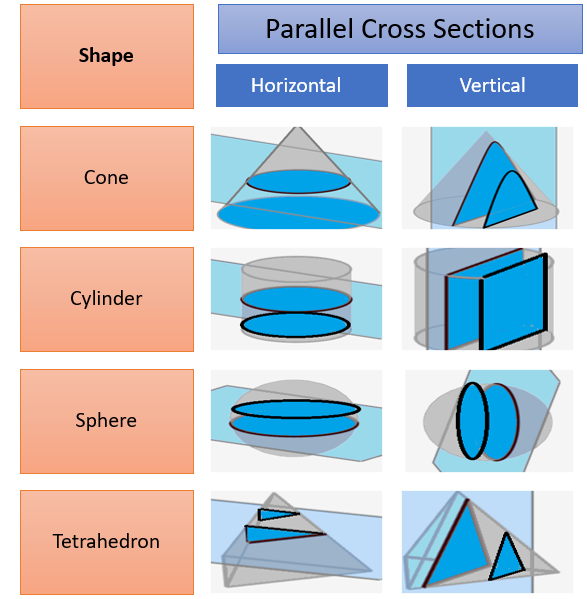
What are Parallel Cross Sections?
Parallel cross sections are repeated cross sections for a solid, parallel to each other. A cross section is what you get when you cut straight through an object.
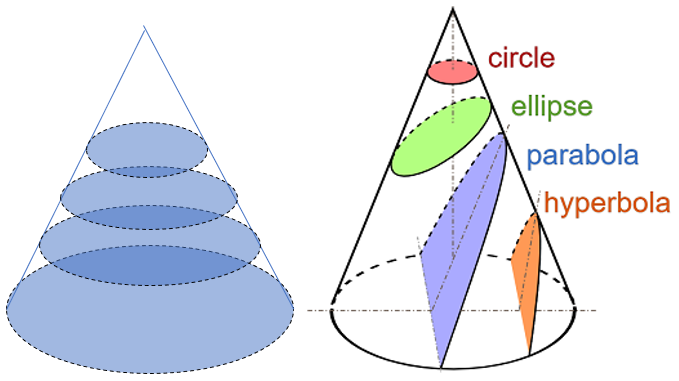
Depending on the shape you’re trying to evenly slice, the parallel cross sections could be circular, elliptical, square or various other shapes. This depends on what direction you take the slices. For example, the following image shows a cone with circular parallel cross sections (left) and several other possible shapes for cross sections (right):
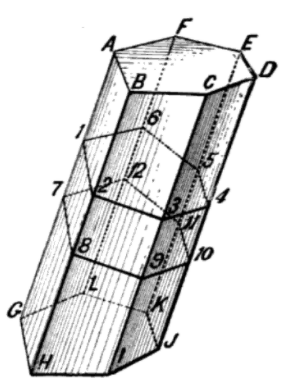
Parallel cross sections can be different sizes (as in the cone above) or equal sizes. For example, if you slice any prism A B C D E F with parallel cross sections, all of the polygons are equal (congruent).
Finding Volume with Parallel Cross Sections
Volumes in calculus are calculated with integrals using parallel cross sections.
Example question: Find the volume of a solid with a circular base and square parallel cross sections perpendicular to the base.
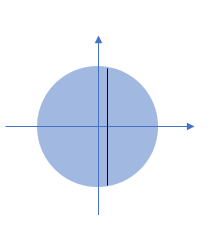
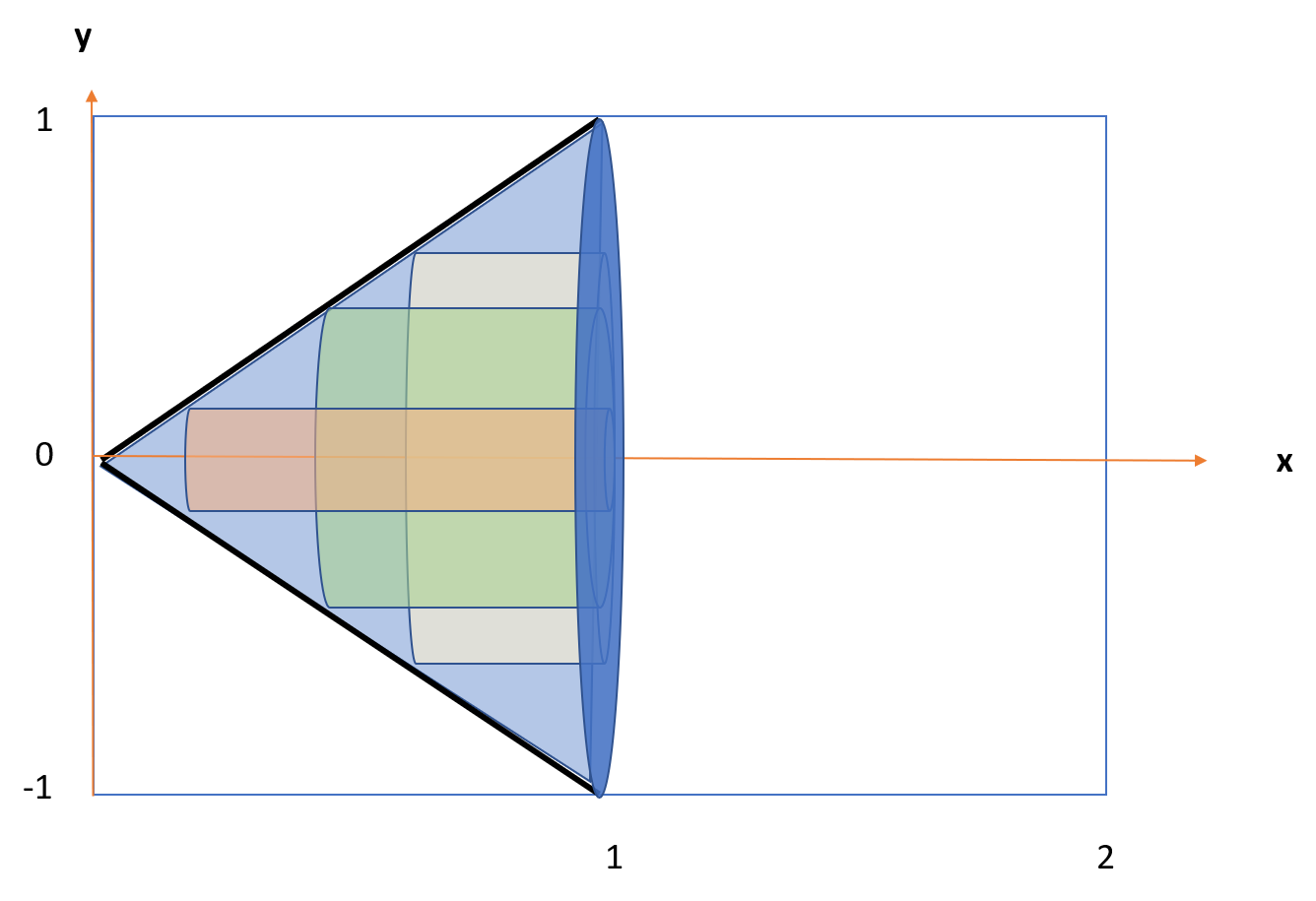
Step 1: Visualize the problem. We’re told that the base is circular and the solid has square parallel cross sections perpendicular to the base. We only need to draw one of these squares, plus the base to visualize the cylinder:

Step 2: Decide which direction you’re going to slice. For a cylinder, we could slice in circles (vertically) or squares (horizontally). Often you have to guess at which way will be easier to integrate. But for this particular question, you’re given a hint: take “square parallel cross sections perpendicular to the base”. We always slice along the x-axis, so the squares need to be aligned with that axis. In the following image, one square is shown as a line, because the thin square is parallel to the y-axis:
Step 3: Set up the integration formula. Here’s where a little knowledge of geometry comes in:
- The top half of the circle is given by the formula y = √(r2 – x2)
- The bottom half of the circle is given by the formula y = -√(r2 – x2)
Given the above formulas, plus that we know the cross sections are squares, we can deduce that the distance of an x (i.e. the side length of a square, one of which is shown as a black line on the image in Step 2) is 2(√(r2 – x2)).
Therefore, the cross-sectional area for any x is given by A(x) = 4(r2 – x2). As x must cover all possible radii (from -r to r), the integral for the volume of the shape is:
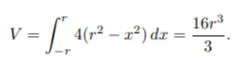
A similar method is the cylindrical shell method to find the volume of a shape. Instead of parallel cross sections, you use very thin shells.
References
Cross sections image: Magister_Mathematicae, CC BY-SA 3.0
Mathematics 116: HWK 8b Solutions §6.2 p463. Retrieved March 2, 2021 from: http://academics.wellesley.edu/Math/Webpage%20Math/Old%20Math%20Site/Math116sontag/Homework/Pdf/hwk8c_solns_f02.pdf