Area of a Bounded Region

Calculus Problem Solving > Area of a Bounded Region

What is a Bounded Region?

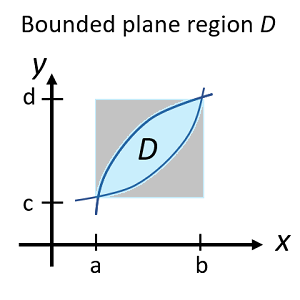
bounded plane region D2 — A bounded region D fitted inside a rectangle.

A bounded region has either a boundary or some set of or constraints placed upon them. In other words, a bounded shape cannot be an infinitely large area—it’s defined by a set of measurements or parameters. A square, drawn on a Cartesian plane, has a natural boundary (four sides). Other shapes and surfaces can be more challenging to visualize. For example, the surface area of a cylinder has constraints of length, height and circumference.

Area of Bounded Region: Worked Example

In integral calculus, if you’re asked to find the area of a bounded region, you’re usually given a set of functions to work with.

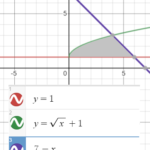
Example question: Find the area of a bounded region defined by the following three functions:

y = 1,
y = √ (x) + 1,
y = 7 – x.

Step 1: Draw the bounded area. I used Desmos.com’s graphing calculator to get an idea of the shape bounded by the three functions:

Step 2: Chop the shape into pieces you can integrate (with respect to x). This is probably the trickiest part of these types of questions.

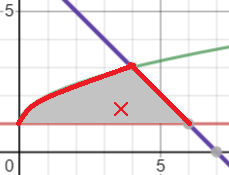
example problem — For this example, you can’t integrate the whole shape because there isn’t a function that starts off as a curve and then drops down in a straight line:

But you *can* integrate the two separate pieces A and B.

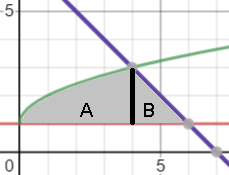
In general, look for regular shapes (triangles, rectangles, squares) or as close to regular shapes as you can get (like the “curvy” triangle A). They should have bases that follows a line horizontal to the x-axis; These shapes are easier to integrate. Caution: Sometimes it’s actually easier to divide the shape up horizontally, instead of the vertical slice shown above. Refer to this pdf (from MIT) for an example of when you would want to slice horizontally.

Step 3: Find the bounds of integration (i.e. the two numbers on the x-axis you’ll be integrating between) for one of the shapes. Let’s start with shape A.

The left-hand bound is easy to see from the graph (x = 0); The right-hand side is x = 4; You can find it with the intersection feature of a graphing calculator or with algebra (See: How to find the intersection of two lines).

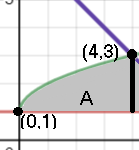
Step 4: Set up the integral, with the bounds you found in Step 3:

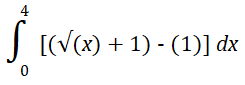
If you’re wondering why I subtracted 1 in the integral, take a look at the following image:

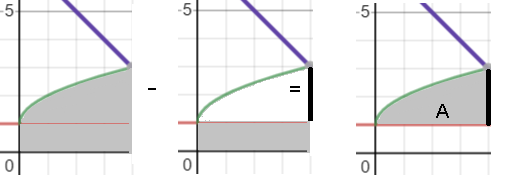
When you integrate √(x) + 1 along the x-axis, you’ll get the entire area on the left. But you need to find the area A on the right; In order to do that, you also have to integrate the function y = 1 then subtract the two areas.

Solving the integral (using the power functions rule and the fact that the integral of a constant function is equal to c x. For example, the integral of f(x) = 10 is 10x). We get an area of 16/3.

Step 5: Repeat steps 3 and 4 for the remaining shapes. For this example we only have one remaining shape (with integral bounds of 4 to 6). Integrating area B, we get 2.

Step 6: Add the areas of all the shapes together.
Area A (16/3) + Area B (2/1) = 22/3.

References

MIT: Find the area between x = y² and y = x – 2. Retrieved September 20, 2020 from: https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/unit-3-the-definite-integral-and-its-applications/part-b-second-fundamental-theorem-areas-volumes/session-56-geometric-interpretation-of-definite-integrals/MIT18_01SCF10_Ses56b.pdf