What is the Tukey Ladder of Powers?
The Tukey ladder of powers (sometimes called the Bulging Rule) is a way to change the shape of a skewed distribution so that it becomes normal or nearly-normal. It can also help to reduce error variability (heteroscedasticity).
Tukey (1977) created a table of powers (numbers to which data can be raised). It’s possible to have an infinite number of powers, but very few are actually in common use. The following table shows the most commonly used transformations, with exponents ranging from -2 to 2.
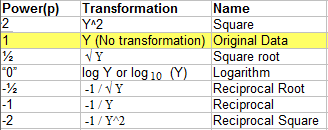
Going up the ladder reduces negative skew. To choose a transformation for negative skew, start with Y2, then plot the data to see how the transformation has affected the data. An exponential function such as Y2 will have a greater effect on larger numbers: 1,000 will become 1,000,000 while 5 will become 25. Due to the fact that y2 increases large numbers by such a massive amount, it’s rare to see transformations above y2.
For positive skews, start with log Y and move down the ladder, plotting as you go to see the effects. Logarithmic functions (with base 10) reduce large numbers more than small numbers. For example, 100,000 reduces to 5 and 100 reduces to 2.
Advantages and Disadvantages
The range of possible transformations with Tukey’s ladder is much more restricted than with the Box Cox transformation. However, the choice of which to use usually boils down to what software you have available (R has both options: transformTukey is in the rcompanion package and boxcox is in the MASS package). Both methods help to minimalize the effects of homoscedastic data, and analysis can theoretically be more accurate if transformations are made. That said, caution should be used when interpreting results from any transformation. What it boils down to is that you have transformed the original data in some way, which means that any analysis performed on the transformed data is not going to give the same results as analysis performed on original data.