Contents:
Euclidean Space
Euclidean Plane
Basic Overview of Euclidean Space
Euclidean space (or Euclidean n-space) is the familiar geometry of shapes and figures that we use to describe our world. It includes three basic constructs that you’re already familiar with: lines, planes and three-dimensional space.

However, it isn’t quite as simple as that (is anything in mathematics?). For example, when you think about how to define a line segment, you can’t just draw a random line on the paper and have it represent all lines. You need to know how long the line is, what point it starts at, and what direction the line is going (forwards? down?). For that, you need vectors. 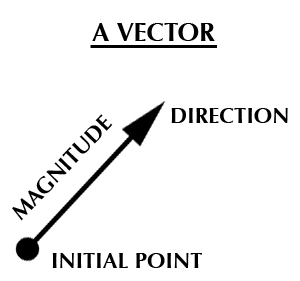
More specifically, you need a real-valued vector. Real-valued vectors have real numbers attached to them, like 26, π, or 0.334.
Formal Definition of Euclidean space
The formal definition of Euclidean space can be written as:
A Euclidean space is a finite-dimensional vector space over the reals &Rpof;, with an inner product <·, ·> (Dieffenbach, 2013)
The basic idea of a finite dimensional vector space is that a finite list of vectors spans across the space. As a simple example, one vector in three dimensional space could be represented by the finite list (7, 2, 9). A “span” is the set of all linear combinations of the list of vectors, so the span of (7, 2, 9) is ((2, 1, 3), (1, 0, 1)).
“Reals” is shorthand for the set of all real numbers. It’s represented by a doublestruck R (&Rpof;). Elements (i.e. the pieces) in Euclidean space are written as follows:
- (x) = one dimensional (in ℝ),
- (x, y) = two-dimensional elements in ℝ2,
- (x, y, z) = three-dimensional elements in ℝ2.
The one-dimensional element (x) is a scalar; Elements of higher spaces (ℝn) are vectors.
Inner product is a generalization of the dot product (·), for multiplying vectors of the same dimension together.
Euclidean Plane Definition, Examples
Euclidean plane geometry is a formal system that characterizes two-dimensional shapes according to angles, distances, and directional relationships. As a form of geometry, it’s the one that you encounter in everyday life and is the first one you’re taught in school. You can think of a Euclidean plane as a sheet of paper, on which you can draw squares, circles, triangles and other 2D shapes and it is a small part of the Euclidean Space (which covers all dimensions from 1D to infinity).
There are two fundamental operations on the plane, called motions. They are translation and rotation, where:
- Translation means that each of our points are shifted in the same direction and by the same distance, or the graph is shrunk or stretched.
- Rotation means that each of our points is turned about a fixed point at the same angles.
Points in a Euclidean plane are often designated by a pair of numbers (x1,x2). As Cartesian coordinates, these are measured in terms of distance from a specified origin and are often called (x,y).
Axioms of Euclidean Plane Geometry
More formally, the Euclidean Plane is a 2 dimensional surface that follows Euclid’s rules, or axioms. You can also think about it as a set of points (or vectors) that satisfy certain relationships. The points are described in terms of:
- Angle: orientation of how two parts meet,
- Direction: left-right sense of parts in relation to one another,
- Distance: lengths and distances between parts.
Two shapes with points and lines showing the same angle, distance, angle, and direction are congruent.
There are just five axioms on which all of Euclidean plane geometry is based. These are:
- Between any two points a straight line can be drawn
- Any line segment (piece of a line) can be extended indefinitely
- Given a point, you can draw a circle centered around it with any given radius.
- All right angles are equal
If any point is not on a line, there is exactly one line through it that does not meet the original line.
It is this last axiom, the parallel postulate, which sets Euclidean space apart from other geometries; and distinguishes the Euclidean plane from other mathematical two-dimensional planes.
References
Banchoff, Thomas. Axioms of Euclidean Plane Geometry. Retrieved from http://www.math.brown.edu/~banchoff/Beyond3d/chapter9/section01.html on March 1, 2019
Dieffenbach, B. (2013). Euclidean Space. Retrieved September 22, 2020 from: https://www.albany.edu/~bd445/Economics_802_Financial_Economics_Slides_Fall_2013/Euclidean_Space.pdf
Jones, Frank. Chapter 1: Euclidean Space. Honors Calculus III/IV Online Textbook. Retrieved from http://www.owlnet.rice.edu/~fjones/chap1.pdf on March 1, 2019
Shurman, J. (2016). Calculus and Analysis in Euclidean Space. Springer International Publishing.
Spelke, E. et al. (2011) Beyond core knowledge: Natural geometry. Retrieved May 20, 2019 from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2897178/