Problem Solving > Vertical shift of a function
What is a Vertical Shift of a Function?
Vertical shift of a function is where the graph of a function moves up or down the y-axis:
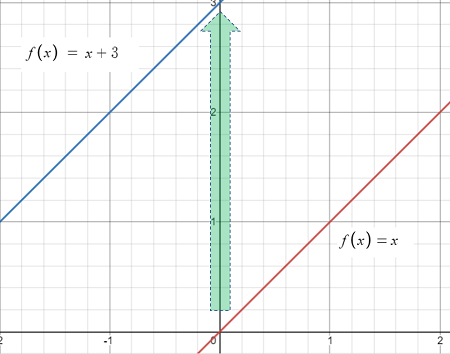
The graph above shows the graph of f(x) = x (in red) shifted up three units from y = 0 to y = 3 (in blue) on the vertical (y) axis. The new graph (blue) is now f(x) = x + 3— the original graph plus the 3 unit shift. This leads to a simple rule for any function:
1. Compared to the graph of f(x), a graph f(x) + k is shifted up k units.
We can also work this in reverse:
2. Compared to the graph of f(x), a graph f(x) – k is shifted down k units.
Generally speaking, a vertical shift adds (or subtracts) a constant to (from) each y-value while leaving the x-value unchanged. In other words, the only changes going on here are y-values moving up or down. The x-values stay exactly where they are.
Vertical Shift of a Function: Examples
Example question #1: How are the graphs of f(x) = |x + 2| and f(x) = |x| related?
Solution:
Step 1: Compare the right hand side of both equations:
- |x + 2|
- |x|.
The difference between these two statements is the “+ 2”.
Step 2: Choose one of the above statements based on the result from Step 1. We have a positive 2, so choose statement 1:
Compared to the graph of f(x), a graph f(x) + k is shifted up k units.
Step 3: Replace the f(x) and f(x) + k the statement with your functions.
Compared to the graph of f(x) = |x|, the vertical shift of a function f(x) = |x + 3| is a shift up 2 units.
Example question #2: How are the graphs of f(x) = 3x2 and f(x) = 3x2 – 8 related?
Solution:
Step 1: Compare the right hand side of both equations:
- 3x2
- 3x2 – 8
The difference between these two statements is the “- 8”.
Step 2: Choose one of the above statements based on the result from Step 1. We have a negative 8, so choose statement 2:
Compared to the graph of f(x), a graph f(x) + k is shifted down k units.
Step 3: Replace the f(x) and f(x) + k the statement with your functions.
Compared to the graph of f(x) = 3x2, the vertical shift of a function f(x) = 3x2 – 8 is a shift down k units.
References
Larson, R. & Edwards, B. (2016). Calculus (10th Edition). Cengage Learning.