A cumulant generating function (CGF) takes the moment of a probability density function and generates the cumulant. A cumulant of a probability distribution is a sequence of numbers that describes the distribution in a useful, compact way.
The first cumulant is the mean, the second the variance, and the third cumulant is the skewness or third central moment.
The CGF is given by:
K(h)= log (M(h))
Were:
- M(t) is the moment generating function.
- log (M(h)) —a logarithmic function—is equal to
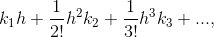
where each of the k1, k2, k3 etc. are the cumulants.
Properties of the Cumulant Generating Function
- The cumulant generating function is infinitely differentiable, and it passes through the origin. Its first derivative is monotonic function from the least to the greatest upper bounds of the probability distribution. Its second derivative is positive everywhere where it is defined.
- Cumulants accumulate: the kth cumulant of a sum of independent random variables is just the sum of the kth cumulants of the summands.
- Cumulants also have a scaling property: the nth cumulant of n X is cn times the nth cumulant of X.
Why the Cumulant Generating Function is Important
The cumulant generating function is important because both it and the cumulants lend themselves so well to mathematical analysis, besides (in the case of the cumulants) being meaningful in their own right. They change in simple, easy to understand ways when their underlying PDF (probability density function) is changed, and they are easy to define on most spaces.
References
Lockhart, R. (2001). Stat 830 Lecture Notes: Generating Functions. Retrieved January 6, 2018 from: from http://people.stat.sfu.ca/~lockhart/richard/830/11_3/lectures/generating_functions/web.pdf.
Wichura, Michael J. (2001). Stat 304 Lecture Notes: Cumulants. Retrieved January 6, 2018 from: https://galton.uchicago.edu/~wichura/Stat304/Handouts/L18.cumulants.pdf