Contents:
- What is a Dependent Event?
- What is an Independent Event?
- Independence of events
- How to tell if an event is Dependent or Independent?
Watch the video for how to tell the difference between dependent and independent events:
What is a Dependent Event?
When two events are dependent events, one event influences the probability of another event. A dependent event is an event that relies on another event to happen first. Dependent events in probability are no different from dependent events in real life: If you want to attend a concert, it might depend on whether you get overtime at work; if you want to visit family out of the country next month, it depends on whether or not you can get a passport in time. More formally, we say that when two events are dependent, the occurrence of one event influences the probability of another event.
Simple examples of dependent events:
- Robbing a bank and going to jail.
- Not paying your power bill on time and having your power cut off.
- Boarding a plane first and finding a good seat.
- Parking illegally and getting a parking ticket. Parking illegally increases your odds of getting a ticket.
- Buying ten lottery tickets and winning the lottery. The more tickets you buy, the greater your odds of winning.
- Driving a car and getting in a traffic accident.
What is an Independent Event?
An independent event is an event that has no connection to another event’s chances of happening (or not happening). In other words, the event has no effect on the probability of another event occurring. Independent events in probability are no different from independent events in real life. Where you work has no effect on what color car you drive. Buying a lottery ticket has no effect on having a child with blue eyes.
When two events are independent, one event does not influence the probability of another event.
Simple examples of independent events:
- Owning a dog and growing your own herb garden.
- Paying off your mortgage early and owning a Chevy Cavalier.
- Winning the lottery and running out of milk.
- Buying a lottery ticket and finding a penny on the floor (your odds of finding a penny does not depend on you buying a lottery ticket).
- Taking a cab home and finding your favorite movie on cable.
- Getting a parking ticket and playing craps at the casino.
What is Independence of Events?

Independence of events means that previous events have no effect on following events. For example, you roll a die once and get a 3; the next roll you get a 4. Neither roll has an effect on each other; they are independent.
Sometimes, it may seem like there is independence of events when in fact there is not. A loaded die, an unfair coin, or lottery balls that have more ink on them (which makes them heavier, and more likely to drop). Card games like poker, also do not have independence of events; the probability of being dealt a particular card changes as the cards are dealt. With a standard deck of cards, your probability of getting an ace is 4/52 (there are four aces, and the standard deck has 52 cards). But if you have already been dealt one card that isn’t an ace, there are 51 cards remaining, which lowers your probability of getting an ace to 4/52.
Checking for Independence of Events
There are four formulas for checking for independence of events:
- P(B | A) = P(B)
- P(A | B) = P(A)
- P(B | A) = P(B | not A)
- P(A and B) = P(A) * P(B)
For example, the probability of getting a heads on a coin flip (we’ll call this event A) is 50% or 0.5. And the probability of a tails (we’ll call this event B) is also 0.5.
Condition 1: P(B | A) = P(B). In English, you would read the left hand side of this equation as “the probability of event B happening, given that event A has happened.” This statement should equal the probability of B.
We know the probability of event B (tails) is 50%, so we need to figure out the left hand side of the equation to compare it. Given that we have already had event A (heads), what is our probability of getting tails? Logic should tell you the probability stays the same: 50%. You could run an experiment by flipping a coin a few thousand times to show that this fact is true, but you don’t need to because of this handy formula.
You don’t actually have to work your way down the list.
If any of these conditions hold, events are independent. That’s because all four equalities are, mathematically speaking, equivalent. Therefore, you only need to check one of these conditions to show that events are independent [1]. The other conditions are useful for figuring out independence if you have other snippets of information about events. For example, you might know the probability of two events happening together (A and B) or you might know the probability of an event not happening (e.g., “not A”).
References
[1] Conditional Probability and Independence.
Dependent or Independent?
Card example

Cards are often used in probability as a tool to explain how one seemingly independent event can influence another. For example, if you choose a card from a deck of 52 cards, your probability of getting a Jack is 4 out of 52. Mathematically, you can write it like this:
P(Jack) = number of Jacks in a deck of cards / total number of cards in a deck = 4/52 = 1/13 ≈ 7.69%.
If you replace the jack and choose again (assuming the cards are shuffled), the events are independent. Your probability remains the same (1/13). Choosing a card over and over again would be an independent event, because each time you choose a card (a “trial” in probability) it’s a separate, non-connected event.
But what if the card was kept out of the pack the next time you choose? Let’s say you pulled the three of hearts, but you’re still searching for that jack. The second time you pull out a card, the deck is now 51 cards, so:
P(Jack) = number of Jacks in a deck of cards / total number of cards in a deck = 4/51 = 1/13 ≈ 7.84%
The probability has increased from 7.69% (with replacement of the jack) to 7.84% (the jack isn’t replaced), so choosing cards in this manner is an example of a dependent event.
How to tell if an event is Dependent or Independent
Being able to tell the difference between a dependent and independent event is vitally important in solving probability questions. Why? Imagine a single event: winning the lotto. That depends upon you buying a ticket. So winning the lotto and buying a ticket are dependent events. Your odds of winning the lotto if you buy a ticket might be 1/1 million. But what about something unrelated, like driving to work and winning the lotto? Your odds of winning the lotto if you drive your car (and don’t buy a ticket) are zero. So the odds change a lot with different event types.
How Can I Figure out what is a Dependent or Independent event?
Figuring out whether events are dependent or independent events can be challenging. Not all situations are as simple as they first appear. For example, you might think that your vote for president increases their chances of winning, but if you consider the Electoral College, that isn’t always the case.

You might think you have a chance of winning the top prize in a scratch off game. But the top prize might have already been won when you buy your ticket. For example, at the time of writing, if you purchased ten, two hundred “$1 Million Monopoly” scratch off tickets in Florida, your chances of winning are exactly the same: Zero!. That’s because 0 out of 15 top prizes are remaining! States like Florida keep a “Remaining Prizes” list…but who really checks it?.
Dependent or Independent? Steps
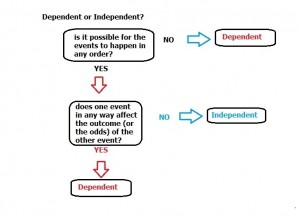
Step 1: Ask yourself, is it possible for the events to happen in any order? If no (the steps must be performed in a certain order), go to Step 3a. If yes (the steps can be performed in any order), go to Step 2. If you are unsure, go to Step 2.
Some examples of events that can clearly be performed in any order are:
- Tossing a coin, then rolling a die.
- Purchasing a car, then purchasing a coat.
- Drawing cards from a deck.
Some events that must be performed in a certain order are:
- Parking and getting a parking ticket (you can’t get a parking ticket without parking).
- Surveying a group of people, and finding out how many women are against gun rights (because you are splitting the survey into subgroups, and you can’t split a survey into subgroups without first performing the survey!).
Step 2: Ask yourself, does one event in any way affect the outcome (or the odds) of the other event? If yes, go to step 3a, if no, go to Step 3b.
Some examples of events that affect the odds or probability of the next event include:
- Choosing a card, not replacing it, then choosing another (because the odds of choosing the first card are 1/52, but if you do not replace it, your are changing the odds to 1/51 for the next draw).
- Choosing anything and not replacing it, then choosing another (i.e. choosing bingo balls, raffle tickets).
Some examples of events that do not affect the odds or probability of the next event occurring are:
- Choosing a card and replacing it, then choosing another card (because the odds of choosing the first card are 1/52, and the odds of choosing the second card are 1/52).
- Choosing anything, as long as you put the items back.
Step 3a: You’re done–the event is dependent.
Step 3b:You’re done–the event is independent.
That’s how to find out if an event is Dependent or Independent!
Dependent or Independent Event Formulas in Probability
There are more formal ways to quantify dependent or independent events. You’ll come across these formulas in basic probability.
P(A|B) = P(A).
P(B|A) = P(B)
The probability of A, given that B has happened, is the same as the probability of A. Likewise, the probability of B, given that A has happened, is the same as the probability of B. This shouldn’t be a surprise, as one event doesn’t affect the other.
You can use the following equation to figure out probability for independent events:
P(A∩B) = P(A) · P(B).
Example:
A poll finds that 72% of Jacksonville consider themselves football fans. If you randomly pick two people from the population, what is the probability the first person is a football fan and the second is as well? That the first one is and the second one isn’t?
Solution: one person being a football fan doesn’t have an effect on whether the second randomly selected person is. Therefore, the events are independent and the probability can be found by multiplying the probabilities together:
First one and second are football fans: P(A∩B) = P(A) · P(B) = .72 * .72 = .5184.
First one is a football fan, the second one isn’t: P(A∩B) = P(A) · P(B) = .72 * 1 – 0.72) = 0.202.
In the second part, I multiplied by the complement. As the probability of being a fan is .72, then the probability of not being a fan is 1 – .72, or .28.
Events A and B are independent if the equation P(A∩B) = P(A) · P(B) holds true. You can use the equation to check if events are independent; multiply the probabilities of the two events together to see if they equal the probability of them both happening together.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education