Statistics Definitions > Location Parameter
What is a Location Parameter?
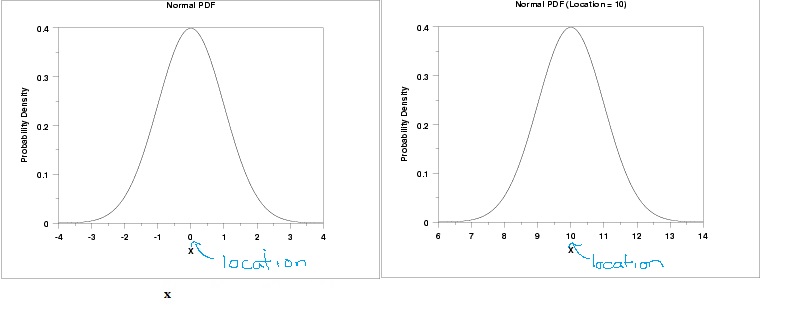
The location parameter tells you where your graph is located. More specifically, it tells you where on the horizontal axis a graph is centered, relative to the standard normal model. The standard normal distribution curve is centered at 0 (the mean), so a parameter of 5 lets you know a graph is centered 5 units to the right of the curve’s center, at x = 5.
The normal distribution curve on the left has a location parameter of 0 and on the right, it’s 10.
A location parameter of -10 moves the graph 5 units to the left of zero, at x = -5.
Relationship to translations in geometry
Location parameters are similar the concept of translations in geometry, where a shape is moved in a certain direction depending on the translation. However, in geometry an object can be translated by angle and distance or by x and y. In statistics, the type of translation defined by the location parameter is only a translation on the x-axis.
Notation
A location family is a set of probability distributions where μ is the location parameter. For example, μ = 9 tells you the center of the graph is located at x = 10.
Mean and Standard Deviation
For the normal distribution, the location parameter is the mean of the data set. However, this is not true for most other distributions.
Location Family
A location family is a class of probability distributions where x0 determines the location of the distribution. Probability density functions or probability mass functions in the location family are defined by the following equation:
Fx0(x) = f(x – x0) where x0 is the location parameter.
If x0 is increased, the graph of the probability function moves to the right on the horizontal axis and if x0 is decreased, the graph moves to the left on the horizontal axis.
Check out our YouTube channel for hundreds of statistics and probability videos from basic stats to advanced stats, Excel and the TI 83/89 calculators.
For errors and corrections in any of our articles or videos, please leave a comment (and thanks in advance!).