Contents:
- Polynomial Function Definition
- Degrees:
- Limits for Polynomial Functions
- Polynomial Sequences
- Extreme Values of a Polynomial
Types of Polynomial Function:
- Bernstein Polynomials
- Chebyshev Polynomials
- Hermite Polynomials
- Homogeneous polynomial
- Orthogonal Polynomials
- Symmetric Polynomials
- Univariate Polynomial
- Zernike Polynomials
- Zero Polynomial
See also: Leading Coefficients.
What is a Polynomial Function?
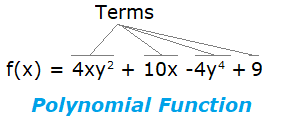
A polynomial function is made up of terms called monomials; If the expression has exactly two monomials it’s called a binomial. The terms can be:
- Constants, like 3 or 523,
- Variables, like a, x, or z,
- A combination of numbers and variables like 88x or 7xyz.
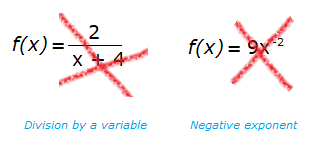
You can’t have:
- Fractional exponents, like x½
- Negative exponents, like x-2
- Variables within the radical (square root) sign. For example, √2.
- Division by a variable.
- An infinite number of terms.
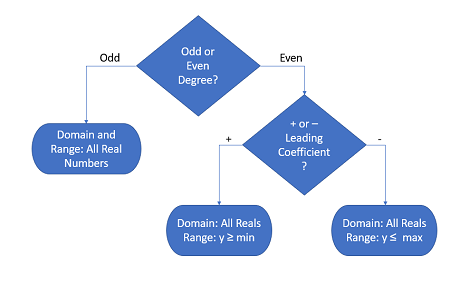
Domain and Range of a Polynomial
The domain and range depends on the degree of the polynomial and the sign of the leading coefficient. Use the following flowchart to determine the range and domain for any polynomial function.
What is a Symmetric Polynomial?
A polynomial is a symmetric polynomial if its variables are unchanged under any permutation (i.e. swap). In other words, if you switch out two of the variables, you end up with the same polynomial.
Examples
The polynomial x + y + z is symmetric because if you switch any of the variables, it remains the same. In other words,
x + y + z = y + z + x = z + x + y
The polynomial x1x3 + 3x1x2x3 is a symmetric polynomial, because if you swap the variables, then it’s still the same polynomial. For example, the following image shows that swapping x1 and x3 results in the same polynomial:
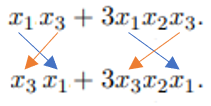
In other words, x1x3 + 3x1x2x3 is the same polynomial as x3x1 + 3x3x2x1
On the other hand, x1x2 + x2x3 is not symmetric. If you swap two of the variables (say, x2 and x3, you get a completely different expression.
Elementary Symmetric Polynomial
Elementary symmetric polynomials (sometimes called elementary symmetric functions) are the building blocks of all symmetric polynomials. For the variables x1, x2, x3,… xn, they are defined mathematically as follows:
- S1 = x1 + x2 + x3 + … + xn
- S2 = x1 x2 + x1 x3 + x1 x4 + … + x(n – 1) x(n – 2)
- S3 = x1 x2 x3 + x1 x2 x4 + … + x(n – 2)x(n – 1)xn
- …
- Sn = x1 x2 x3 … xn
As an example, the elementary symmetric polynomials for the variables x1, x2 and x3 are:
- S1 = x1 + x2 + x3
- S2 = x1 x2 + x1 x3 + x2 x3
- S3 = x1 x2 x3
Graphs of a Symmetric Polynomial
They are called “symmetric” not because their graph shows symmetry, but because they remain the same if you permute their roots. As far as graphing, the graph of any symmetric polynomial would look exactly the same no matter which variables you switch around. If the graph changes, then the expression is not symmetric.
Why are Symmetric Polynomials Important?
Symmetric polynomials are particularly important in number theory because two types—the elementary symmetric and power sum symmetric polynomials can completely represent any set of points in the set of all complex numbers.
See also: Testing for Symmetry of a Function.
Univariate Polynomial
A univariate polynomial has one variable—usually x or t. For example, P(x) = 4x2 + 2x – 9.In common usage, they are sometimes just called “polynomials”.
For real-valued polynomials, the general form is:
Zernike Polynomials
Zernike polynomials are sets of orthonormal functions that describe optical aberrations; Sometimes these polynomials describe the whole aberration and sometimes they describe a part. For example, “myopia with astigmatism” could be described as ρ cos 2(θ). This description doesn’t quantify the aberration: in order to so that, you would need the complete Rx, which describes both the aberration and its magnitude. Different polynomials can be added together to describe multiple aberrations of the eye (Jagerman, 2007).
Zernike polynomials aren’t the only way to describe abberations: Seidel polynomials can do the same thing, but they are not as easy to work with and are less reliable than Zernike polynomials.
Extreme Values of a Polynomial
Extreme values of a polynomial are the peaks and valleys of the polynomial—the points where direction changes.
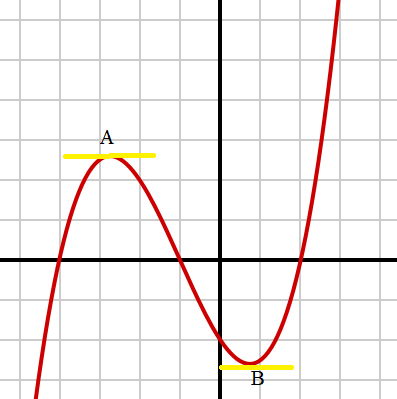
The peaks and valleys are called relative (local) maxima and minima.
- On a graph, you find extreme values by looking to see where there’s a mountain top (“peak”) or valley floor.
- Mathematically, you find them by looking at the derivative. At an extreme point, where there is a direction change, the derivative of the function is zero.
Note: the derivative is the slope of the tangent line. In the above graph, the tangent line is horizontal, so it has a slope (derivative) of zero.
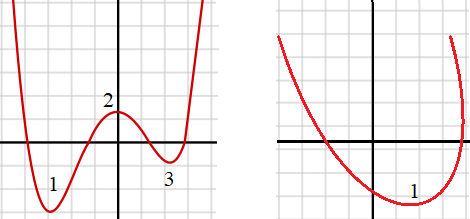
The Number of Extreme Values of a Polynomial
Polynomials can be classified by degree. This comes in handy when finding extreme values. A polynomial of degree n can have as many as n – 1 extreme values. For example, a 4th degree polynomial has 4 – 1 = 3 extremes.
This follows directly from the fact that at an extremum, the derivative of the function is zero. If a polynomial is of n degrees, its derivative has n – 1 degrees. For example, take the 2nd degree polynomial 3x2. The derivative (using the power rule) is the first degree polynomial, 6x.
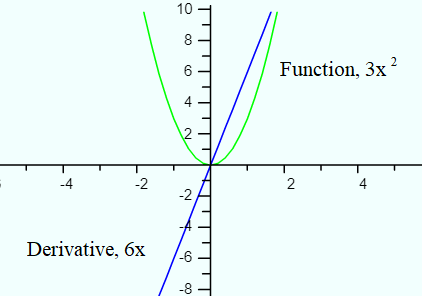
The above image demonstrates an important result of the fundamental theorem of algebra: a polynomial of degree n has at most n roots. Roots (or zeros of a function) are where the function crosses the x-axis; for a derivative, these are the extrema of its parent polynomial.
Note that the polynomial of degree n doesn’t necessarily have n – 1 extreme values—that’s just the upper limit. The actual number of extreme values will always be n – a, where a is an odd number.
Absolute Extreme Values of Polynomials
The absolute extreme values (also known as the global extreme values) of a polynomial are the absolute maxima and minima of the polynomial. These are the points where the function takes its largest and smallest values, period.
An absolute extreme value is also a relative extreme value.
To find the absolute extreme values of a polynomial:
- Find all extreme values for the entire range,
- Calculate the value of the polynomial at each of the extremes.
- Find the value of the polynomial at the endpoints of the range.
The point at which the polynomial is largest is the absolute maximum value; the point at which our polynomial is smallest is the absolute minimum value.
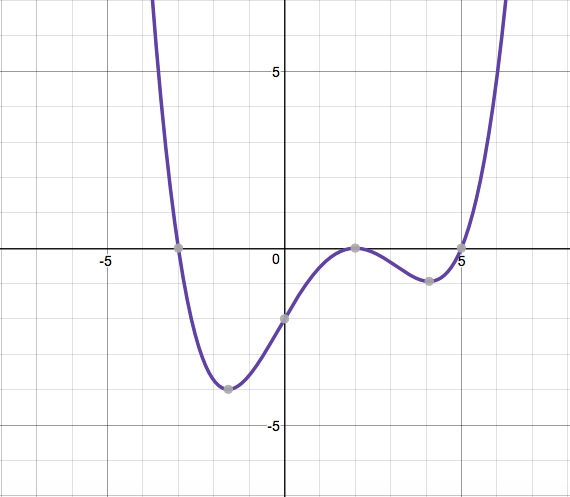
You can also simply graph the polynomial and make a visual judgement. In the image below, the polynomial has a relative maxima at 2 and relative minima at 4 and -2. The relative minima at -2 is also a global minima; the absolute maxima doesn’t exist because the value of the polynomial goes toward positive infinity at both ends.
Bernstein Polynomials
Bernstein Polynomials as Approximations of Functions
Bernstein polynomials, named after Russian mathematician, Sergei Natanovich Bernstein, are a way to approximate the core ingredients of functions.
These polynomials converge (settle on) a particular function of choice, giving good approximations with very few combined Bernstein polynomials. Another advantage is that by using a set of polynomials, rather than a function, points can be calculated and stored efficiently [1]. One disadvantage is that the classic Bernstein polynomials tend to converge slowly [2], a fact that caused them to “languish in obscurity” until the advent of the modern computer [3].
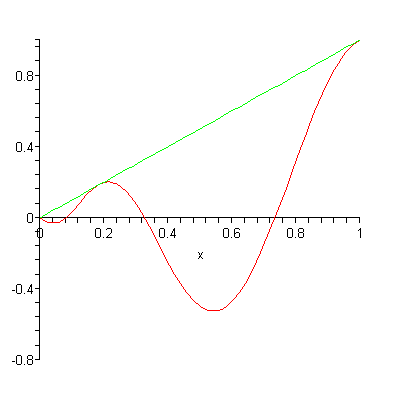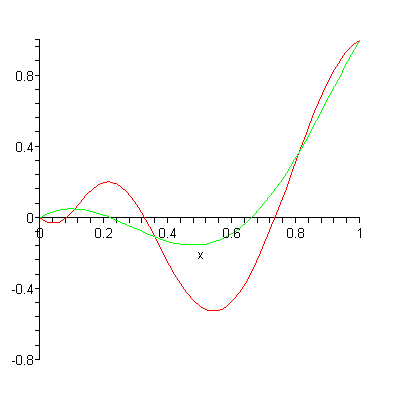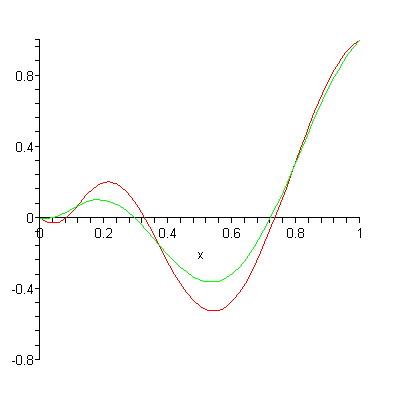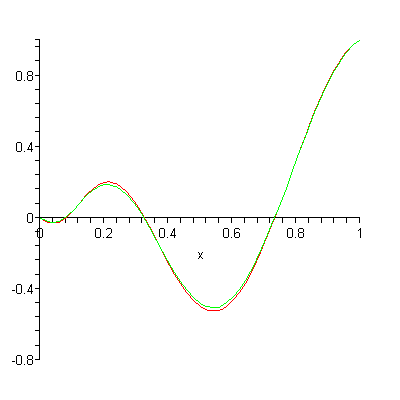
In many situations, it’s better to use Bernstein polynomials rather than an explicit function of the form y = f(x), because of the limitations of function notation. These include the fact that a vertical line (i.e. a vertical asymptote) x = c cannot be described using function notation.
Formula
A Bernstein polynomial of degree n is a linear combination of the (n + 1) Bernstein basis polynomials of degree n. The n + 1 Bernstein basis polynomials of degree n are defined as:
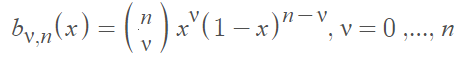
Where ![]() is a binomial coefficient.
is a binomial coefficient.
Every Bernstein basis polynomial is nonnegative on [0,1], and zero only at the endpoints [3].
Practical Uses of a Bernstein Polynomial Function
Bernstein polynomials are used in statistics for smoothing and as a basis for Bezier elements used in isogeometric analysis [4]. They form the mathematical foundation for computer-aided geometric design (CAGD); Adobe’s Illustrator and Flash, as well as font imaging systems like Postscript; all use Bernstein polynomials to create Bezier curves— a type of parametric curve.
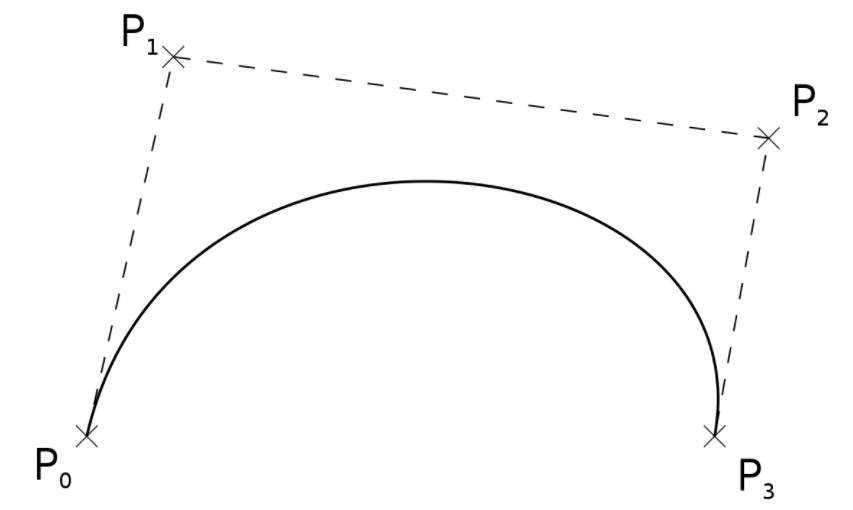
Bernstein Polynomial Function: References
[1] Timmerman, G. (2014). Approximating Continuous Functions and Curves&hellip Retrieved July 15, 2021 from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.754.2049&rep=rep1&type=pdfhttps://sites.math.washington.edu/~morrow/336_14/papers/grant.pdf
[2] Guan, Z. Iterated Bernstein polynomial approximations. Retrieved July 15, 2021 from:
[3] BERNSTEIN_POLYNOMIAL. Retrieved July 15, 2021 from: https://people.sc.fsu.edu/~jburkardt/f_src/bernstein_polynomial/bernstein_polynomial.html
[4] Farouki, R. The Bernstein polynomial basis: A centennial retrospective. Computer Aided Geometric Design. Volume 29, Issue 6, August 2012, Pages 379-419. Retrieved July 15, 2021 from: https://www.sciencedirect.com/science/article/abs/pii/S0167839612000192
Chebyshev Polynomials
Chebyshev polynomials crop up in many areas of calculus, including numerical integration, orthogonal polynomials and spectral methods for partial differential equations. They can also be used for curve fitting (finding a function that models a curve), interpolation and in multiple other areas of numerical analysis.
The general formula for a Chebyshev polynomial, for an integer n ≥ 0, is:
Tn(x) = cos(n cos-1x) ; -1 ≤ x ≤ 1
Properties
For n ≥ 2 (Smith, 2011):
- Tn(x) is an n th-order polynomial in x.
- When n is an even integer, Tn(x) is an even function.
- When n is an odd integer, Tn(x) is an odd function.
- Tn(x) has n zeros in the open interval (-1, 1).
- Tn(x) has n + 1 extrema in the closed interval [-1, 1].
Chebyshev Polynomials of the First Kind
Some authors refer to Chebyshev polynomials as just the Chebyshev polynomial of the first kind (Tn)—a polynomial in x of degree n, defined by the relation (Mason & Handscomb, 2002):
Tn(x) = cos nθ when x = cosθ.
The following table (Culham, 2020) lists the first 12 Chebyshev Polynomials of the first kind, obtained from Rodrigue’s formula:
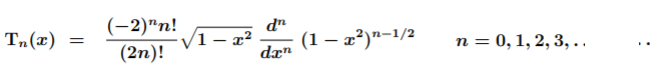
| T0(x) = 1 |
| T1(x) = x |
| T2(x) = 2x2 – 1 |
| T3(x) = 4x3 – 3x |
| T4(x) = 8x4 – 8x2 + 1 |
| T5(x) = 16x5 – 20x3 + 5x |
| T6(x) = 32x6 – 48x4 + 18x2 – 1 |
| T7(x) = 64x7 – 112x5 + 56x3 – 7x |
| T8(x) = 128x8 – 256x6 + 160x4 – 32x2 + 1 |
| T9(x) = 256x9 – 576x7 + 432x5 – 120x3 + 9x |
| T10(x) = 512x10 – 1280x8 + 1120x6 – 400x4 + 50x2 – 1 |
| T11(x) = 1024x11 – 2816x9 + 2616x7 – 1232x5 + 220x3 – 11x |
Hermite Polynomial Function
Hermite polynomials are a widely used family of polynomials, defined over (-∞, ∞), with a weight function proportional to w(x) = e-x2.
Definition of Hermite Polynomials
There are several definitions for “Hermite polynomials”, which can be a source of confusion. First, two different starting points result in two different sets of polynomials, often called the “physicists” and “probabilists'” polynomials. Most authors simply refer to Hermite polynomials without any clarification, assuming the reader is working in one field or another (i.e. physics or probability) and therefore don’t need to know the “other” definition.
If you’re in calculus, you’re likely dealing with the “physicists” Hermite polynomials, built from the monomials. The first few are (Sawitzki, 2009):
- H0 (x) = 1
- H1 (x) = x
- H2 (x) = x2 – 1
- H3 (x) = x3 – 3x
- H4 (x) = x4 – 6x2 + 3
- H5 (x) = x5 – 10x3 + 15x
- H6 (x) = x6 – 15x4 + 45x2 – 15
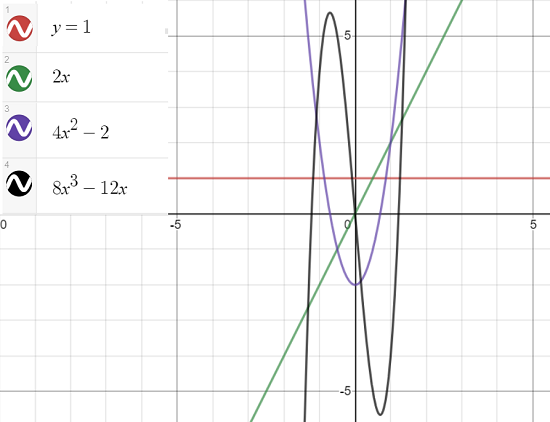
An alternate definition, with w(x) = e-x2/2 is sometimes used, especially in statistics. The “probabilists'” polynomials are sometimes called Chebyshev-Hermite polynomials (Sawitzki, 2009). The first few are:
- H0 (x) = 1
- H1 (x) = 2x
- H2 (x) = 4x2 – 2
- H3 (x) = 8x3 – 12x
- H4 (x) = 16x4 – 48x2 + 12
- H5 (x) = 32x5 – 160x3 + 120x
- H6 (x) = 64x6 – 480x4 + 720x2 – 120
Hermite Interpolation and Other Uses
Hermite polynomials are very useful as interpolation functions because their value—and their derivatives values— up to order n are unity at zero at the endpoints of the closed interval [0, 1] (Huebner et al., 2001). They provide an alternative way of representing cubic curves, allowing the curve to be defined in terms of endpoints and derivatives at those endpoints (Buss, 2003).
Hermite polynomials occur in various areas of physics, including as part of the solution to the quantum harmonic oscillator Hamiltonian. They also arise in numerical analysis as Gaussian quadrature.
Homogeneous polynomial
A homogeneous polynomial is a multivariate polynomial (i.e. a polynomial of more than one variable), with all terms of the same degree. Another way to put this: a polynomial is homogeneous of degree d if it is a linear combination of monomials of degree d [1].
General homogeneous polynomials are sometimes called polynomial forms:
- Degree 1 is a linear form,
- Degree 2 is a quadratic form,
- Degree 3 is a cubic form.
A homogeneous polynomial of degree k is also a homogeneous function of degree k. However, the converse is not true: there are many homogeneous functions that are not polynomials.
Homogeneous Polynomial Examples
A more simple definition of a homogeneous polynomial is that that the sum of the exponents of the variables is the same for every term. For example, x3 + y3 = z3 or x2y3 = z5). The most famous example of a homogeneous polynomial is the Pythagorean theorem x2 + y2 = z2.
The expression x5 + 4x3y2 + 8xy4 is a homogeneous polynomial of degree 5. The sum of the exponents for each term gives you the degree of the term:
- x5 = 5
- 4x3y2 = 3 + 2 = 5
- 8xy4 = 8x1y4 = 4 + 1 = 5.
The product of two or more homogeneous polynomials is also a homogeneous polynomial, with a degree equal to the sum of the factor’s degrees. If all of the factors are not homogeneous, then the product is also not homogeneous. If the polynomial factors aren’t homogeneous, then neither is the product.
A homogeneous polynomial can be also be represented by a symmetric matrix. A symmetric matrix is a square matrix with symmetry around its leading diagonal, from top left to bottom right, as if you were folding along the diagonal. The top right half of the matrix and the bottom left half are mirror images about the diagonal. The following matrix represents Ax2 + 2Bxy + Dy2 [2]:
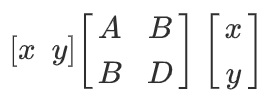
References
[1] Bertram, A. Polynomials. Math 4800/6080 Project Course. Retrieved August 6, 2021 from: https://www.math.utah.edu/~bertram/4800/PolyIntroduction.pdf
[2] Blinn, J. (2003). Consider the Lowly 2 x 2 Matrix. In Jim Blinn’s Corner.
Orthogonal Polynomials
Orthogonal polynomials (also called an orthogonal polynomial sequence) are a set of polynomials that are orthogonal (perpendicular, or at right angles) to each other.
As a simple example, the two-dimensional coordinates {x, y} are perpendicular to each other. So two polynomials that each fit along the x and y axes are orthogonal to each other. When we talk about “orthogonal polynomials” though, we actually mean an orthogonal polynomial sequence. In other words, there must be an infinite number of them in order to meet the formal definition.
Formal Definition
Orthogonal polynomials are the infinite sequence:
p0 (x), p1 (x), p2 (x), … pn (x),
Where:
- pn(x) is a polynomial with degree n,
- Any two polynomials are orthogonal to each other.
This can be represented by the following integral, which basically means if you multiply the two functions and integrate the result is zero:
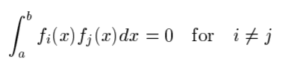
The closed interval [a, b] is called the interval of orthogonality; The interval can be infinite at one end, or both.
As an example, of what this integral means, the following image shows the separate integration of two orthogonal polynomials ½(3x2 – 1) and ½(5x3 – 3x) on the closed interval [-1, 1]:
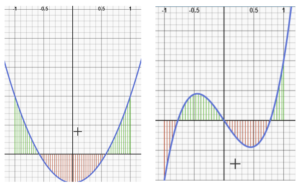
It should come as no surprise then, that the two integrals, when multiplied together on the same interval (see: integration by parts), also equal zero.
Examples of Orthogonal Polynomials
The above two integrals (graphed with Integral-Calculator) are a part of a sequence called Legendre polynomials, which form solutions to the Legendre differential equation. Another set of orthogonal polynomials which are widely used are Hermite polynomials, which are part of the solution to the quantum harmonic oscillator Hamiltonian.
Degrees of a Polynomial Function
“Degrees of a polynomial” refers to the highest degree of each term. To find the degree of a polynomial:
- Add up the values for the exponents for each individual term.
- Choose the sum with the highest degree.
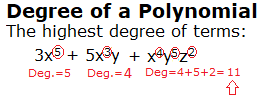
First Degree Polynomial Function
First degree polynomials have terms with a maximum degree of 1. In other words, you wouldn’t usually find any exponents in the terms of a first degree polynomial. For example, the following are first degree polynomials:
- 2x + 1,
- xyz + 50,
- 10a + 4b + 20.
The shape of the graph of a first degree polynomial is a straight line (although note that the line can’t be horizontal or vertical). The linear function f(x) = mx + b is an example of a first degree polynomial.
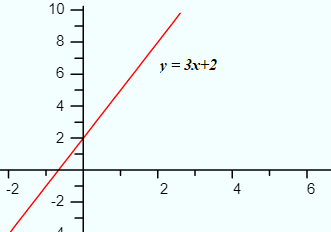
First degree polynomials have the following additional characteristics:
- A single root, solvable with a rational equation.
- A constant rate of change with no extreme values or inflection points.
- The entire graph can be drawn with just two points (one at the beginning and one at the end).
- Symmetry for every point and line.
- The range is the set of all real numbers.
Second Degree Polynomial Function
Second degree polynomials have at least one second degree term in the expression (e.g. 2x2, a2, xyz2). There are no higher terms (like x3 or abc5). The quadratic function f(x) = ax2 + bx + c is an example of a second degree polynomial.
The graphs of second degree polynomials have one fundamental shape: a curve that either looks like a cup (U), or an upside down cup that looks like a cap (∩).
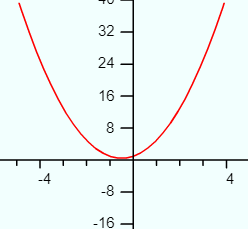
Second degree polynomials have these additional features:
- One extreme value (the vertex). A line of symmetry through the vertex.
- Zero inflection points.
- They take three points to construct; Unlike the first degree polynomial, the three points do not lie on the same plane.
- Up to 2 roots.
Third Degree Polynomial
A cubic function (or third-degree polynomial) can be written as:
![]()
where a, b, c, and d are constant terms, and a is nonzero.
Unlike quadratic functions, which always are graphed as parabolas, cubic functions take on several different shapes. We can figure out the shape if we know how many roots, critical points and inflection points the function has.
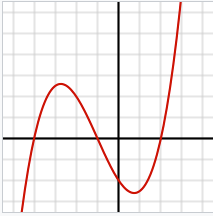
Third degree polynomials have been studied for a long time. In fact, Babylonian cuneiform tablets have tables for calculating cubes and cube roots. Chinese and Greek scholars also puzzled over cubic functions, and later mathematicians built upon their work.
Roots and Critical Points of a Cubic Function
Let’s suppose you have a cubic function f(x) and set f(x) = 0. Together, they form a cubic equation:
![]()
The solutions of this equation are called the roots of the polynomial. There can be up to three real roots; if a, b, c, and d are all real numbers, the function has at least one real root.
The critical points of the function are at points where the first derivative is zero:
![]()
We can use the quadratic equation to solve this, and we’d get:
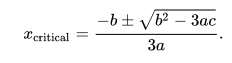
It’s actually the part of that expression within the square root sign that tells us what kind of critical points our function has. Suppose the expression inside the square root sign was positive. Then we’d know our cubic function has a local maximum and a local minimum.
If b2-3ac is 0, then the function would have just one critical point, which happens to also be an inflection point. An inflection point is a point where the function changes concavity.
What about if the expression inside the square root sign was less than zero? Then we have no critical points whatsoever, and our cubic function is a monotonic function.
Limit for a Polynomial Function
There’s more than one way to skin a cat, and there are multiple ways to find a limit for polynomial functions. This can be extremely confusing if you’re new to calculus. But the good news is—if one way doesn’t make sense to you (say, numerically), you can usually try another way (e.g. graphically).
You can find a limit for polynomial functions or radical functions in three main ways:
Graphical and numerical methods work for all types of functions; Click on the above links for a general overview of using those methods. All work well to find limits for polynomial functions (or radical functions) that are very simple. You might also be able to use direct substitution to find limits, which is a very easy method for simple functions; However, you can’t use that method if you have a complicated function (like f(x) + g(x)).
This next section walks you through finding limits algebraically using Properties of limits . Properties of limits are short cuts to finding limits. They give you rules—very specific ways to find a limit for a more complicated function. For example, you can find limits for functions that are added, subtracted, multiplied or divided together.
Limit for a Polynomial Function (Algebraic Method)
Example problem: What is the limit at x = 2 for the function
f(x) = (x2 +√2x)?
Step 1: Look at the Properties of Limits rules and identify the rule that is related to the type of function you have. The function given in this question is a combination of a polynomial function ((x2) and a radical function ( √ 2x). It’s what’s called an additive function, f(x) + g(x). The rule that applies (found in the properties of limits list) is:
lim x→a [ f(x) ± g(x) ] = lim1 ± lim2
Step 2: Insert your function into the rule you identified in Step 1.
lim x→2 [ (x2 + √ 2x) ] = lim x→2 (x2) + lim x→2(√ 2x).
Step 3: Evaluate the limits for the parts of the function. If you’ve broken your function into parts, in most cases you can find the limit with direct substitution:
lim x→2 [ (x2 + √2x) ] = (22 + √2(2) = 4 + 2
Step 4: Perform the addition (or subtraction, or whatever the rule indicates):
lim x→2 [ (x2 + √2x) ] = 4 + 2 = 6
That’s it!
Back to Top
Polynomial Sequences
A polynomial sequence can be generated by various degree polynomials. As there are an infinite number of any particular type of polynomial, there are an infinite number of possible polynomial sequences.
Examples:
These sequences are usually integer valued (i.e. their inputs are 1, 2, 3, …).
Examples:
| Degree | Generating Function | Polynomial Sequence |
| 1 | f(x) = 3x | {3, 6, 9,…} |
| 2 | f(x) = 2x2 | {2, 8, 18, 32, …} |
| 3 | f(x) = 4x3 | {4, 32, 108, 256, …} |
| 4 | f(x) = x4 + 1 | {2, 17, 82, 257, …} |
| 5 | f(x) = x5 – 99 | {-98, -67, 144, 925, …} |
Finding a Generating Polynomial Function for a Polynomial Sequence
One way to identify the generating polynomial function is to plot points on a graph.
Example question: What function generates the polynomial sequence {0, 1, 4, 7,…}?
Solution:
Step 1: Make a table of x and y values. Your x-values are the places of each term (1, 2, 3, 4) and your y-values are the terms of the sequence: {0, 1, 4, 7,…}.
| x | y |
| 1 | 0 |
| 2 | 1 |
| 3 | 4 |
| 4 | 7 |
Step 2: Sketch a graph of the points from Step 1:
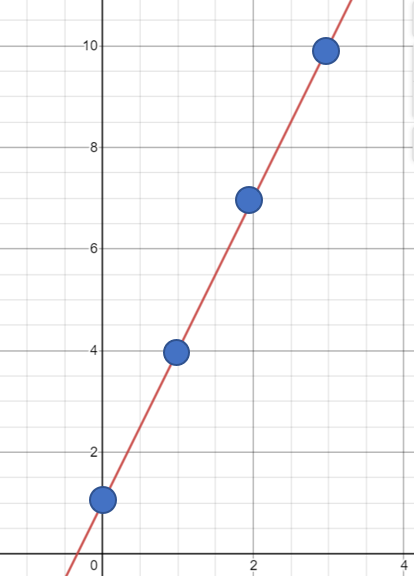
Step 3: Find the formula: From the graph, it’s clear that this sequence is generated by a linear function. The formula for a linear function is y = mx + b.
The slope is the common difference between the points. The common difference is 3, so m = 3.
“b” is the y-intercept. For this graph, it looks like that’s at 1. So our formula is:
f(x) = 3x + 1
Step 4: Test a couple of points in the formula. Plugging in a couple of points to the formula will confirm the formula you found in Step 3 is correct.
- f(0) = 3(0) + 1 = 1
- f(1) = 3(1) + 1 = 4.
The polynomial function generating the sequence is f(x) = 3x + 1.
That’s it!
finding the Degree of the Generating Polynomial Function
Finding the common difference is the key to finding out which degree polynomial function generated any particular sequence. In general, keep taking differences until you get a constant in a row. The number of times you have to take differences is the degree of your polynomial.
Example question: What is the degree of the polynomial that generated the sequence {2, 8, 18, 32}?
Solution: Find the differences between terms:
6 10 14
And again:
6 6.
We had to find the common difference twice to get a constant row, so the polynomial sequence {2, 8, 18, 32} was generated by a second-degree polynomial.
Zero Polynomial
What is a Zero Polynomial Function?
The zero polynomial function (also called the zero function) has several different definitions, depending on the author. For example, it is sometimes defined as a polynomial with degree of 0 (where the degree of a polynomial is the largest exponent of any term with a nonzero coefficient). However, it could also mean:
- A degree of -1.
- A degree of infinity (∞),
- An undefined degree (i.e., no degree is assigned to it),
- Simply the function f(x) = 0.
- A formal sum with all zero coefficients (by convention, -∞); This comes about because when all of a polynomials coefficients are zero (sometimes called “padding” with zero terms), the polynomial disappears and becomes f = 0,
One reason for these different definitions is a matter of convenience: depending on what mathematical operation you’re performing, you may want to assign the zero polynomial a degree of -1 or -∞, but as neither of these functions are easy to manipulate it’s usually easier just to leave its degree undefined.
A non-zero polynomial functionhas a degree of 1 or more (not including infinity).
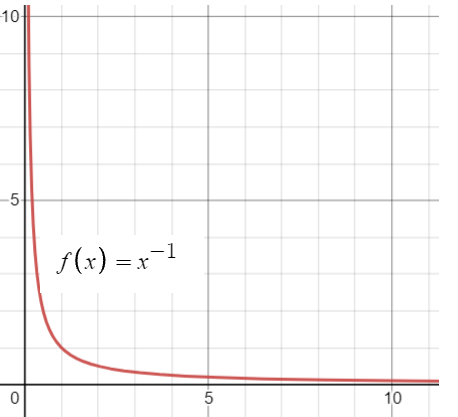
A Special Property of the Zero Polynomial
The zero polynomial function has a special property: it is the only polynomial function that has a function value that becomes close to zero as x gets sufficiently large.
Zero Polynomial: References
Image created with Desmos.com.
[1] University of Utah. Mathematics 1010 online: Polynomials. Retrieved October 24, 2021 from: https://www.math.utah.edu/online/1010/poly/
[2] Aspnes, J. (2003). Polynomials. Retrieved October 24, 2021 from: https://www.cs.yale.edu/homes/aspnes/pinewiki/Polynomials.html
[3] Polynomial.java. Retrieved October 24, 2021 from: https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/Polynomial.java.html
[4] Bertram. Polynomial Basics. Retrieved October 24, 2021 from: https://www.math.utah.edu/~bertram/courses/4030/Polys.pdf
[5] Rings of Polynomials. Retrieved October 24, 2021 from: https://www.math.uci.edu/~ndonalds/math120b/2poly.pdf
Back to Top
Polynomial Function: References
Graph: Desmos.com.
Arfken, G. “Orthogonal Polynomials.” Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 520-521, 1985.
Aufmann, R. et al. (2005).Intermediate Algebra: An Applied Approach. Cengage Learning.
Buss, S. (2003). 3D Computer Graphics. A Mathematical Introduction with OpenGL. Cambridge University Press.
Culham, J. (2020). Chebyshev Polynomials. Retrieved August 22, 2020 from: mhtl.uwaterloo.ca/courses/me755/web_chap6.pdf
Davidson, J. (1998). First Degree Polynomials. Retrieved 10/20/2018 from: https://www.sscc.edu/home/jdavidso/Math/Catalog/Polynomials/First/First.html
Egge, E. (2018). Combinatorics of Symmetric Functions. Retrieved December 2, 2019 from: https://d31kydh6n6r5j5.cloudfront.net/uploads/sites/66/2019/04/eggecompsdescription.pdf
Huebner, K. et al. (2001). The Finite Element Method for Engineers. Wiley.
Iseri, Howard. Lecture Notes:
Shapes of Cubic Functions. MA 1165 – Lecture 05. Retrieved from http://faculty.mansfield.edu/hiseri/Old%20Courses/SP2009/MA1165/1165L05.pdf
Iyanaga, S. and Kawada, Y. (Eds.). “Systems of Orthogonal Functions.” Appendix A, Table 20 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980
Orthogonal Polynomials. Retrieved February 12, 2020 from: https://sydney.edu.au/science/chemistry/~mjtj/CHEM3117/Resources/poly_etc.pdf
Jagerman, L. (2007). Ophthalmologists, Meet Zernike and Fourier! Trafford Publishing.
Mason, J. & Handscomb, S. (2002). Chebyshev Polynomials. CRC Press.
Mario123. Symmetric Polynomials. Retrieved December 2, 2019 from: file:///C:/Users/brit6/Downloads/Symmetric%20Polynomials.pdf
Negrinho, R. (2013). Shape Representation Via Symmetric Polynomials: a Complete Invariant Inspired by the Bispectrum. Retrieved December 2, 2019 from: https://www.cs.cmu.edu/~negrinho/assets/papers/msc_thesis.pdf
Parillo, P. (2006). MIT 6.972 Algebraic techniques and semidefinite optimization. Retrieved September 26, 2020 from: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-972-algebraic-techniques-and-semidefinite-optimization-spring-2006/lecture-notes/lecture_05.pdf
Sansone, G. Orthogonal Functions. New York: Dover, 1991
Sawitzki, G. (2009). Computational Statistics: An Introduction to R, CRC Press.
Smith, J.O. Spectral Audio Signal Processing, http://ccrma.stanford.edu/~jos/sasp/, online book, 2011 edition, accessed August 23, 2020.
Singhal, M. (2017). Generalizations of Hall-Littlewood Polynomials. Retrieved December 2, 2019 from: https://math.mit.edu/research/highschool/primes/materials/2017/conf/5-4-Singhal.pdf