What is a Constant Term?
A constant term in an expression or equation contains no variables. In other words, it’s just number on its own. For example:
f(x) = 2x2 + 3 (the constant term is 3).
Other examples of constant terms: 5, -99, 1.2 and pi (π = 3.14…).
Linear Function
In the linear function y = f(x) = a + bx, the constant term (actually the y-intercept) is a.
Polynomials
Varying the constant term in a polynomial function moves the function up or down. The following image (graphed with Desmos) shows how changing the last term of y = 2x2 + a moves the function on the y-axis:
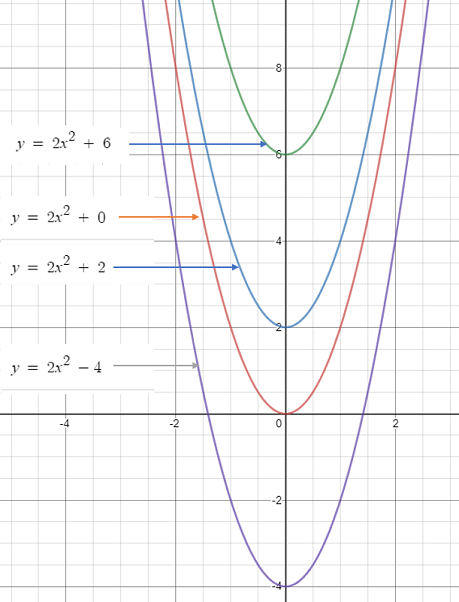
Quadratic functions aren’t much different. The form of this particular function is:
f(x) = ax2 + bx + c, where a, b, and c are constants.
While there are three constants in this expression, the only term that’s on its own (i.e. without a variable attached) is “c”, so that is the constant term.
Power Series
The first term in a power series is a constant term. The general power series can be defined as:
f(x) = c0 + c1x + c2x + c3x + c4x + …
As you might be able to tell, the only constant on its own (i.e. without an “x”) is the first term. For a power series, the constant term is what results from substituting x = 0 into the formula. For example, let’s say you have the following equation for a power series:
f(x) = 3 + 5x + 7x2 + 9x3 + 11x4 + ….
Substituting x = 0, we get:
f(x) = 3 + 5(0) + 7(0)2 + 9(0)3 + 11(0)4 + ….
= 3.
Derivative of a Constant Term
The derivative of any constant is zero. For example, if you have a basic function like y = 15, this graphs as a horizontal line and therefore has a zero slope.
See: Derivative of a Constant..