Finding Limits with Direct Substitution
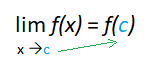 Direct substitution is just what the name implies: you directly substitute a given value into a limit.
Direct substitution is just what the name implies: you directly substitute a given value into a limit.
Probably the most intuitive way to find a limit is to look at a limit graphically (on a graphing calculator) or numerically (through a table). However, in some cases it’s actually easier—and faster—to find a limit with direct substitution. If you’ve ever put a specific value into an equation in algebra (like putting x = 2 into the function y = x + 10), then you have already performed direct substitution. It’s really that easy!
When to Use Direct Substitution
Direct substitution works well when you have a simple functions with additions, subtractions, divisions, multiplications, powers and roots.

For example, this technique can work with constant functions, like:
- f(x) = 10,
- f(x) = 6,
- f(x) = 99.99.
You can also use it to find limits for linear functions, which produce straight lines in a graph; they have “x” as the input variable and the “x” has an exponent of one. Examples of linear functions are:
- f(x) = x,
- f(x) = 2x – 2,
- f(x) = x + 1.
When NOT to use direct substitution: If you plug in x-values (using the steps below) and get an indeterminate limit (either 0/0 or ∞/∞), you can’t use this technique. Use the dividing out technique for limits instead.
Find Limits with Direct Substitution: Steps
Example problem 1:
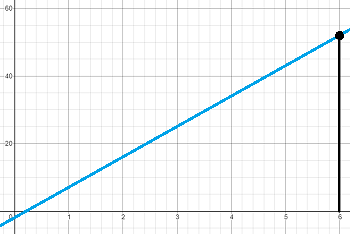
Find the limit of f(x) = 9x – 2 at x = 6.
Step 1: Make sure the function as a simple function (one of the types shown in the above image). This particular function is made up of sums, so we can use the rule.
Step 2: Substitute the “x” value (the point at which you want to find the limit) into the function. In this example, you’re looking for the limit at x = 6, so:
f(x) = 9x – 2
f(x) = 9(6) – 2
f(x) = 54 – 2
f(x) = 52
The limit of f(x) = 9x – 2 as x approaches 6 is 52.
A quick look at a graph of f(x) = 9x – 2 shows this is the correct answer:
Example 2
Find the limit of f(x) = √(x) at x = 4
Step 1: Make sure the function as a simple function. This is a radical function, so we can use the rule.
Step 2: Substitute the “x” value into the function. In this example, you’re looking for the limit at x = 4, so:
√(4) = 2
The limit of f(x) = √(x) as x approaches 4 is 2.
Example 3
This next example may look a little more complicated, but it isn’t: you’re still just “filling in the blanks.”
Find the limit:
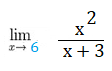
Step 1: Make sure the function as a simple function. This is a radical function, so we can use the rule.
Step 2: Substitute the “x” value into the function. In this example, you’re looking for the limit at x = 6, so:
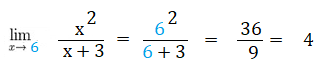
The limit as x approaches 6 is 4.
Polynomials and Radicals
Direct substitution can also work for polynomial functions and radical functions, as long as you are sure the function is defined at the x-value you want to find the limit at. For example, you can use direct substitution for all values of f(x) = 1/x, except at 0 (because division by zero is undefined). If your algebra isn’t strong, a good rule of thumb is that you shouldn’t use direct substitution to solve for the limit unless you are sure that the function is defined for all real numbers.
References
Berresford, G. & Rockett, A. (2015). Applied Calculus. Cengage Learning.