The term “linear form” has a few different meanings in math and calculus. The exact definition depends on where you are using it:
1. Linear Form (Equations for a Line)
An equation is in linear form if it is written as y = mx + b. Informally speaking, that’s an “equation for a line.”
If a line can be represented by the equation Ax + By + C = 0, then the equation is a general (or standard) linear form for the line [1].
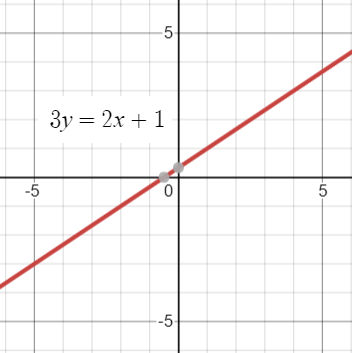
Non-linear equations can be converted to linear forms. Watch the video, which shows you how:
Linear forms don’t have to be straight lines though. A homogeneous polynomial (which is a multivariate polynomial with terms of the same degree) of degree 1 is a polynomial linear form. The most well-known example of a homogeneous polynomial is the Pythagorean theorem x2 + y2 = z2. Trigonometric functions can also linear (in the sense of a form), as long as the trig functions are raised no higher than the 1st power [2].
An affine function is sometimes defined as a linear Form plus a number. Generally, when dealing with affine functions, they can be expressed with a slightly different format:
c1x1 + … + cnxn.
Adding a constant to this expression gives the affine function:
c1x1 + … + cnxn + b
Mathematical relationships can also have a linear form. For example, two sets of data might closely follow each other in a linear relationship, detectable with a Correlation Coefficient.
2. Differential Equations in “Linear Form”
If a differential equation is in the form:
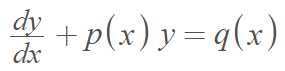
then it is in linear form.
3. Other Areas of Math
Many other areas of math use the term to describe a specific behavior or format. For example, a linear map for a given vector space E over a field K, f: E → K, is called a linear form; The set of all of these linear forms is called the dual space of E [3].
References
[1] Chung, S. Understanding Basic Calculus. Retrieved October 10, 2021 from: http://www.math.nagoya-u.ac.jp/~richard/teaching/f2016/BasicCalculus.pdf
[2] Patel, A. Section 6.2 Trigonometric Equations PART 1. Retrieved October 10, 2021 from: http://apps.lonestar.edu/blogs/apatella/files/2014/08/section-62-2.pdf
[3] 17.1 Hyperplanes and Linear Forms. Retrieved October 10, 2021 from: https://www.cis.upenn.edu/~cis610/geombchap17.pdf